<メモ>
放射性崩壊と半減期
これはゲームAIの判断に利用できそう。おそらく出来る
確率論的な式で見た指数グラフ
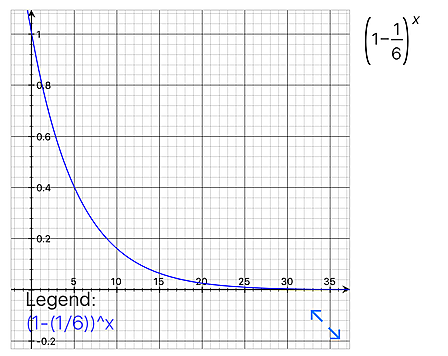
半減期(halflife)的な式で見た指数グラフ
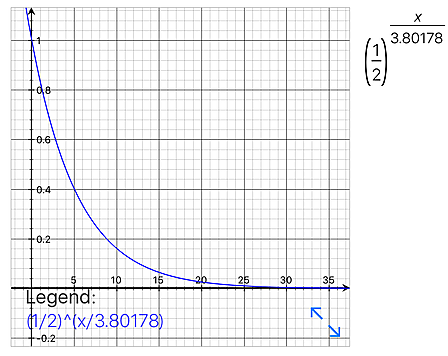
自然対数(napier)的な式で見た指数グラフ
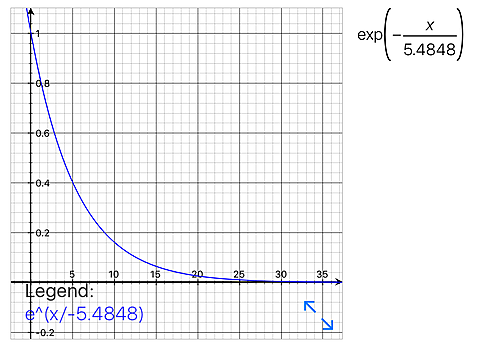
式が扱う題材、目的はどれも違うがグラフ形状自体はまったく同じものに出来る
ゲームに利用される確率がある段階まで急激に変化し、ある段階で安定しだしたりするのは「この形状」が原因と考えられる
ネイピア数 
\(e=\lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ n } \right) }^{ n } } \quad にx乗した式\quad { e }^{ x }=\lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ n } \right) }^{ nx } } \\ この式に対しN=nxとして\\ { e }^{ x }=\lim _{ N\rightarrow \infty }{ { \left( 1+\frac { 1 }{ n } \right) }^{ N } } \quad 、n=\frac { N }{ x } なので{ e }^{ x }=\lim _{ N\rightarrow \infty }{ { \left( 1+\frac { x }{ N } \right) }^{ N } } \\ ここでマクローリン展開(テイラー展開)する。{ \left( a+b \right) }^{ n }に従うような二項定理を利用しながら式にすると\\ { e }^{ x }=\lim _{ N\rightarrow \infty }{ \sum _{ r=0 }^{ N }{ { _{ N }{ C }_{ r } } } \cdot { 1 }^{ N-r }\cdot { \left( \frac { x }{ N } \right) }^{ r } } \quad となる。これを計算すると\\ \\ { e }^{ x }=\lim _{ N\rightarrow \infty }{ { _{ N }{ C }_{ 0 } } } { \left( \frac { x }{ N } \right) }^{ 0 }+{ _{ N }{ C }_{ 1 } }{ \left( \frac { x }{ N } \right) }^{ 1 }+{ _{ N }{ C }_{ 2 } }{ \left( \frac { x }{ N } \right) }^{ 2 }+{ _{ N }{ C }_{ 3 } }{ \left( \frac { x }{ N } \right) }^{ 3 }+{ _{ N }{ C }_{ 4 } }{ \left( \frac { x }{ N } \right) }^{ 4 }+\cdots \\ =\lim _{ N\rightarrow \infty }{ 1 } +x+\frac { N\left( N-1 \right) }{ 2! } \cdot \frac { { x }^{ 2 } }{ { N }^{ 2 } } +\frac { N\left( N-1 \right) \left( N-2 \right) }{ 3! } \cdot \frac { { x }^{ 3 } }{ { N }^{ 3 } } +\frac { N\left( N-1 \right) \left( N-2 \right) \left( N-3 \right) }{ 4! } \cdot \frac { { x }^{ 4 } }{ { N }^{ 4 } } \cdots \\ =\lim _{ N\rightarrow \infty }{ 1 } +x+\frac { \frac { { N }^{ 2 }-N }{ { N }^{ 2 } } { x }^{ 2 } }{ 2! } +\frac { \frac { { N }^{ 3 }-3{ N }^{ 2 }+2N }{ { N }^{ 3 } } { x }^{ 3 } }{ 3! } +\frac { \frac { { N }^{ 4 }-6{ N }^{ 3 }+11{ N }^{ 2 }-6N }{ { N }^{ 4 } } { x }^{ 4 } }{ 4! } \cdots \\ =\lim _{ N\rightarrow \infty }{ 1 } +x+\frac { \left( 1-\frac { 1 }{ { N }^{ 2 } } \right) { x }^{ 2 } }{ 2! } +\frac { \left( 1-\frac { 3 }{ { N } } +\frac { 2 }{ { N }^{ 2 } } \right) { x }^{ 3 } }{ 3! } +\frac { \left( 1-\frac { 6 }{ { N } } +\frac { 11 }{ { N }^{ 2 } } -\frac { 6 }{ { N }^{ 3 } } \right) { x }^{ 4 } }{ 4! } \cdots \quad =\quad 1+x+\frac { \left( 1-0 \right) { x }^{ 2 } }{ 2! } +\frac { \left( 1-0+0 \right) { x }^{ 3 } }{ 3! } +\frac { \left( 1-0+0-0 \right) { x }^{ 4 } }{ 4! } \cdots \\ =1+x+\frac { { x }^{ 2 } }{ 2! } +\frac { { x }^{ 3 } }{ 3! } +\frac { { x }^{ 4 } }{ 4! } \cdots \)