原始n乗根（ド・モアブルの定理）

原始n乗根

<虚数の情緒P469の詳細>

原始5乗根の解を求める。解くべき方程式は\({ x }^{ 5 }-1=0 \)　である
5次の方程式の解は5つある
5次の多項式の根は5つある

この式から導かれる解の一つは、すぐに解る
\(x=1\quad \Leftrightarrow \quad { x }-1=0\)
これを足掛かりに5次の多項式を因数分解していく
\( (x-1)\div ({ x }^{ 5 }-1)\quad =\quad { x }^{ 4 }+{ x }^{ 3 }+{ x }^{ 2 }+{ x }+1\)
原始n乗根、円分方程式、「多項式の割り算」の計算パターンとして、この形はよく出てくるので憶えておくといい

多項式の割り算は以下のように行える

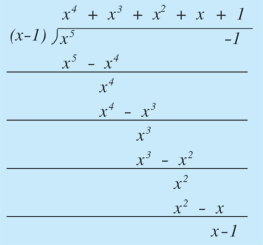
\(({ x }^{ 5 }-1)\quad \Leftrightarrow \quad (x-1)({ x }^{ 4 }+{ x }^{ 3 }+{ x }^{ 2 }+{ x }+1)\quad \Leftrightarrow \quad (x-1){ \cdot x }^{ 2 }\cdot ({ x }^{ 2 }+{ x }+{ 1+{ \frac { 1 }{ x } } }+\frac { 1 }{ { x }^{ 2 } } )\)
第三項目に注目して解く。パラメータtを設定する
\(t=x+\frac { 1 }{ x } \quad \) として \(\quad ({ x }^{ 2 }+{ x }^{ 1 }+{ 1+{ \frac { 1 }{ x } } }+\frac { 1 }{ { x }^{ 2 } } )\quad =\quad { t }^{ 2 }+t-1\)

根の公式 \(\frac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a } \) を利用して \({ t }^{ 2 }+t-1\) を因数分解すると \(t=\frac { -1\pm \sqrt { 5 } }{ 2 }\) となり
\( ({ x }^{ 5 }-1)\quad \Leftrightarrow \quad (x-1){ \cdot x }^{ 2 }\cdot ({ t }^{ 2 }+t-1)\quad \Leftrightarrow \quad (x-1){ \cdot x }^{ 2 }\cdot \left( t-\frac { -1+\sqrt { 5 } }{ 2 } \right) \cdot \left( t-\frac { -1-\sqrt { 5 } }{ 2 } \right) \)

この式に\(t=x+\frac { 1 }{ x }\) を再代入して二次方程式に誘導する
\( (x-1){ \cdot x }\cdot \left( x+\frac { 1 }{ x } +\frac { 1-\sqrt { 5 } }{ 2 } \right) { \cdot x }\cdot \left( x+\frac { 1 }{ x } +\frac { 1+\sqrt { 5 } }{ 2 } \right) \quad \Leftrightarrow \quad (x-1)\left( { x }^{ 2 }+\frac { 1 }{ 2 } \left( 1-\sqrt { 5 } \right) x+1 \right) \left( { x }^{ 2 }+\frac { 1 }{ 2 } \left( 1+\sqrt { 5 } \right) x+1 \right) \)

もう一度、根の公式を利用して第二三項目を解く

\( { x }^{ 2 }+\frac { 1 }{ 2 } \left( 1-\sqrt { 5 } \right) x+1\) を根の公式で処理

\({ x }_{ 2,3 }=\frac { \frac { 1 }{ 2 } \left( -1+\sqrt { 5 } \right) \pm \sqrt { { \left( \frac { 1-\sqrt { 5 } }{ 2 } \right) }^{ 2 }-4\times 1\times 1 } }{ 2\times 1 } =\frac { \frac { 1 }{ 2 } \left( -1+\sqrt { 5 } \right) \pm \sqrt { \frac { 6-2\sqrt { 5 } }{ 4 } -\frac { 16 }{ 4 } } }{ 2 } =\frac { \frac { 1 }{ 2 } \left( -1+\sqrt { 5 } \right) \pm \frac { 1 }{ 2 } i\sqrt { 10+2\sqrt { 5 } } }{ 2 } =\frac { 1 }{ 4 } \left( \sqrt { 5 } -1\pm i\sqrt { 10+2\sqrt { 5 } } \right) \)

\( { x }^{ 2 }+\frac { 1 }{ 2 } \left( 1+\sqrt { 5 } \right) x+1\) を根の公式で処理

\({ x }_{ 4,5 }=\frac { \frac { 1 }{ 2 } \left( -1-\sqrt { 5 } \right) \pm \sqrt { { \left( \frac { 1+\sqrt { 5 } }{ 2 } \right) }^{ 2 }-4\times 1\times 1 } }{ 2\times 1 } =\frac { \frac { 1 }{ 2 } \left( -1-\sqrt { 5 } \right) \pm \sqrt { \frac { 6+2\sqrt { 5 } }{ 4 } -\frac { 16 }{ 4 } } }{ 2 } =\frac { \frac { 1 }{ 2 } \left( -1-\sqrt { 5 } \right) \pm \frac { 1 }{ 2 } i\sqrt { 10-2\sqrt { 5 } } }{ 2 } =\frac { 1 }{ 4 } \left( -\sqrt { 5 } -1\pm i\sqrt { 10-2\sqrt { 5 } } \right) \)

結果的に因数分解はこうなる

\(({ x }^{ 5 }-1)\quad \Leftrightarrow \quad (x-1)\left( x-\frac { 1 }{ 4 } \left\{ \sqrt { 5 } -1+i\sqrt { 10+2\sqrt { 5 } } \right\} \right) \left( x-\frac { 1 }{ 4 } \left\{ \sqrt { 5 } -1-i\sqrt { 10+2\sqrt { 5 } } \right\} \right) \left( x-\frac { 1 }{ 4 } \left\{ -\sqrt { 5 } -1+i\sqrt { 10-2\sqrt { 5 } } \right\} \right) \left( x-\frac { 1 }{ 4 } \left\{ -\sqrt { 5 } -1-i\sqrt { 10-2\sqrt { 5 } } \right\} \right) \)

＜pocketCasでの計算結果＞

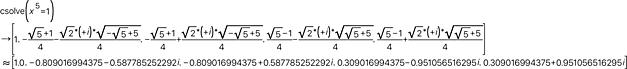
複素数の実数部と虚数部の計算は以下になる
\({ x }_{ 1 }=\overbrace { 1 }^{ 実数部 } +\overbrace { 0i }^{ 虚数部 } \\ { x }_{ 2 }=\frac { 1 }{ 4 } \left\{ \sqrt { 5 } -1+i\sqrt { 10+2\sqrt { 5 } } \right\} \quad =\quad \frac { \sqrt { 5 } -1 }{ 4 } +\frac { i\sqrt { 10+2\sqrt { 5 } } }{ 4 } \quad =\quad \overbrace { 0.3090... }^{ 実数部 } +\overbrace { 0.9510...i }^{ 虚数部 } \\ { x }_{ 3 }=\frac { 1 }{ 4 } \left\{ \sqrt { 5 } -1-i\sqrt { 10+2\sqrt { 5 } } \right\} \quad =\quad \frac { \sqrt { 5 } -1 }{ 4 } -\frac { i\sqrt { 10+2\sqrt { 5 } } }{ 4 } \quad =\quad 0.3090...-0.9510...i\\ { x }_{ 4 }=\frac { 1 }{ 4 } \left\{ -\sqrt { 5 } -1+i\sqrt { 10+2\sqrt { 5 } } \right\} \quad =\quad \frac { -\sqrt { 5 } -1 }{ 4 } +\frac { i\sqrt { 10-2\sqrt { 5 } } }{ 4 } \quad =\quad -0.8090...+0.5877...i\\ { x }_{ 5 }=\frac { 1 }{ 4 } \left\{ -\sqrt { 5 } -1-i\sqrt { 10+2\sqrt { 5 } } \right\} \quad =\quad \frac { -\sqrt { 5 } -1 }{ 4 } -\frac { i\sqrt { 10-2\sqrt { 5 } } }{ 4 } \quad =\quad -0.8090...-0.5877...i\)

この因数分解後の根（複素数）を複素平面（ガウス平面）にマッピングする
実数と虚数部をそれぞれ算出してグラフ上に点を置くと単位円周上に等間隔の点が打たれ正五角形になることが確認できる

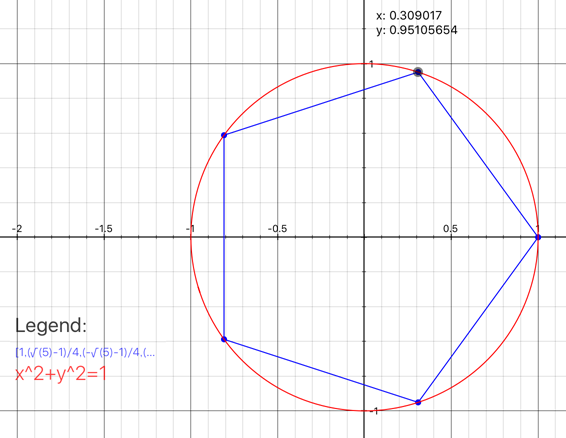
ちなみに円周360°を五角形で割ると360/5=72
ラジアンでなく分度器などの度（オイラー角と呼ばれる）でサインコサインを計算させると以下になる
\(\sin { (72) } =0.9510...\\ \cos { (72)=0.3090... } \)

ラジアンで書くとこうなる
\(\sin { \frac { 2\pi \cdot 1 }{ 5 } } =0.9510...\\ \cos { \frac { 2\pi \cdot 1 }{ 5 } } =0.3090...\)

この事から因数分解の式は以下のように書ける事にもなる

\(\left( { x }^{ 5 }-1 \right) =\left\{ x-\left( \cos { \frac { 2\pi \cdot 1 }{ 5 } } +\sin { \frac { 2\pi \cdot 1 }{ 5 } } i \right) \right\} \cdot \left\{ x-\left( \cos { \frac { 2\pi \cdot 2 }{ 5 } } +\sin { \frac { 2\pi \cdot 2 }{ 5 } } i \right) \right\} \cdot \left\{ x-\left( \cos { \frac { 2\pi \cdot 3 }{ 5 } } +\sin { \frac { 2\pi \cdot 3 }{ 5 } } i \right) \right\} \cdot \left\{ x-\left( \cos { \frac { 2\pi \cdot 4 }{ 5 } } +\sin { \frac { 2\pi \cdot 4 }{ 5 } } i \right) \right\} \cdot \left\{ x-\left( \cos { \frac { 2\pi \cdot 5 }{ 5 } } +\sin { \frac { 2\pi \cdot 5 }{ 5 } } i \right) \right\} \\ =\left\{ x-\left( 0.3090+0.9510i \right) \right\} \cdot \left\{ x-\left( -0.8090+0.5877i \right) \right\} \cdot \left\{ x-\left( -0.8090-0.5877i \right) \right\} \cdot \left\{ x-\left( 0.3090-0.9510i \right) \right\} \cdot \left\{ x-\left( 1+0i \right) \right\} \)

これはド・モアブルの定理と呼ばれる計算手法になっている