イプシロンデルタ論法の機能考察 [微積分と物理/イプシロンデルタ論法の機能考察]

\(\forall \varepsilon >0\quad (\quad \exists \delta >0\quad (\quad \forall n\in \mathbb{N}\quad (\quad n>\delta \quad \Rightarrow \quad \left| { a }_{ n }-\alpha \right| <\varepsilon \quad ))))\quad \)

この論理式の処理手続きを図にすると以下になる

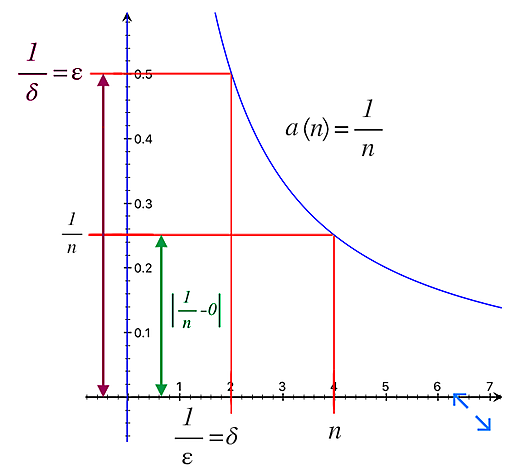
プログラムであれば、コードの処理方法と扱うパラメータの意味を知っておく必要がある。以下にその意味を整理すると

コードは括弧の内側から左から右へと順に処理される。この件の場合「\(n>\delta \)」から処理が始まる
\({a}_{n}\)と\(n\)は入出力の関係。\({ a }_{ n }=a\left( n \right) =\frac { 1 }{ n } \)。数学的に言えば\(n\)は定義域。\({a}_{n}\)は値域になっている（グラフ図の横軸値、縦軸値の関係になっている）
\(\varepsilon\)と\(\delta\)は入出力の関係。\(\delta\)は定義域。\(\varepsilon\)は値域になっている。任意の正の数\(\varepsilon\)が与えられたとして、その\(\varepsilon\)に対応する正の数\(\delta\)を見つけようとすると、その\(\delta\)は\(\varepsilon\)を利用した逆関数となる。（この\(\varepsilon\)と\(\delta\)は絶対値で考える必要がある。つまりグラフで見たとき距離として扱う必要がある点に留意）
~~\(\varepsilon\)と\(\delta\)は正の数に縛り付けているのでグラフ第一象限のみを考えればいい~~ 左記は間違い。論理式を読むと絶対値による「＋－の距離」を考える必要がある。今回の件に関して言えば第三象限にあるグラフに対しても同じように考える必要がある

各命題の意味は以下になる

\(\forall \varepsilon >0\)	0という下界を持つ単調増減少させることが出来る任意の正の数\(\varepsilon\)
\(\exists \delta >0\)	0という下界を持つ単調増減少させることが出来る選ばれた正の数\(\delta\)。又、\(\varepsilon\)と対応する関係（相互に関数関係）にあるこの論証を成立させる\(\delta\)は\(\displaystyle \lim _{ n\rightarrow \infty }{ \frac { 1 }{ n } } =0\)　より \(\displaystyle \delta =\frac { 1 }{ \varepsilon } \)と定義できる
\(\forall n\in \mathbb{N}\)	これは\(\forall \varepsilon >0\)を考えた時、きめの粗い考え方になってしまう。しかし\(\displaystyle \lim _{ n\rightarrow \infty }{ \frac { 1 }{ n } } =0\)　を\(n\)に対応する数列\(｜ { a }_{ n } ｜\)と考える際に役に立つ考え方である。例えばデデキント切断等を考える場合は有理数の集合を扱うのでこのようにした方が扱いやすい。本件に関しては問題が出ないのでこのようになっている。本来ここは　\(\forall n>0\)　と書くのが0を除いた正の実数でよりふさわしい

TODO

\(n>\delta\)
\(\Rightarrow ｜ { a }_{ n } ｜ <\varepsilon \)

\(n\)は\(\delta\)を下界として単調増加する。これは\(n\)のカウントアップが\(\delta\)に依存している事を示している
ならば\(｜ { a }_{ n } ｜ \)は\(\varepsilon\)を上界として単調減少する（\(\alpha\)は\(0\)なので省略しています）

\(\displaystyle \lim _{ n\rightarrow \infty }{ \frac { 1 }{ n } } =0\)　は\(n\)を無限大\(\infty\)にした際、\(\frac { 1 }{ n }\)は\(0\)に収束する事を表している
\(\alpha=0\)として考えた際、\(n\)に対応する数列\(\left| { a }_{ n } \right| \)が\(0\)を下界として単調減少する事を説明できれば収束を証明できた事になる

数列の単調減少とは、すなわち任意の\(n=1,2,3...\)において\({a}_{n-1}>{a}_{n}\)が成り立つ
数列の下界が\(0\)とは、すなわち任意の\(n=1,2,3...\)において\({a}_{n}>0\)が成り立つ

＜収束の証明手順まとめ＞

数列が単調増加（単調減少）する事を証明する
数列が上界（下界）を持つ事を証明する

単調減少や下界は数の大小関係で説明できる。数の大小とは「ふたつの数」が必要となる（ひとつの数では比較対象がいないので、ものの大小すら論じる事が出来ない）
\({a}_{n}\)と\(n\)という2軸上の点をなにかと比較したい時、\(\varepsilon\)と\(\delta\)という2軸上の点という比較対象が必要となる

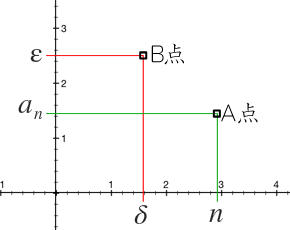
つまり\(\varepsilon\)と\(\delta\)は「一つ隣の点」と言える。数列で言えば\({a}_{n}\)の隣、\({a}_{n+1}\)や\({a}_{n-1}\)となりえる
これと比較すれば証明が出来る

証明

\({a}_{n}\)と\(n\)、\(\varepsilon\)と\(\delta\)は対応する関係にある

\({ a }_{ n }=\frac { 1 }{ n } \quad ,\quad n=\frac { 1 }{ { a }_{ n } } \quad ,\quad \varepsilon =\frac { 1 }{ \delta } \quad ,\quad \delta =\frac { 1 }{ \varepsilon } \)

\(n>\delta , \exists \delta >0\)　より　\(n>\delta>0\)　となる。又、

\(\forall \varepsilon >0 , \left| { a }_{ n } \right| <\varepsilon \)　より　\(0<\left| { a }_{ n } \right| <\varepsilon\)　となる

これを踏まえて\(\varepsilon\delta\)を「一つ隣の点（unityのC#で例えればVector2型の配列で一つ隣）」と考えると

\(\varepsilon =\left\{ \varepsilon は\forall \varepsilon >0と\varepsilon =\frac { 1 }{ \delta } を満たし0を下界とする1以下の単調減少する数である \right\} =\left\{ 1,\frac { 1 }{ 2 } ,\frac { 1 }{ 3 } ,\frac { 1 }{ 4 } ... \right\} =\left\{ 限りなく0に近づき小さくなっていく数列 \right\} \)

\(\delta =\left\{ \delta は\exists \delta >0と\delta =\frac { 1 }{ \varepsilon } を満たし0を下界とする単調増加する数である \right\} =\left\{ 1,2,3,4... \right\} =\left\{ 無限に大きくなっていく数列 \right\} \)

\(n=\left\{ n>\delta \right\} =\left\{ 2,3,4,5... \right\} =\left\{ \delta により下から押し上げられ無限に大きくなっていく数列 \right\} \)

\({ a }_{ n }=\left\{ \frac { 1 }{ n } \right\} =\left\{ \frac { 1 }{ 2 } ,\frac { 1 }{ 3 } ,\frac { 1 }{ 4 } ,\frac { 1 }{ 5 } ... \right\} =\left\{ 0<\left| { a }_{ n } \right| <\varepsilon より\varepsilon で頭は押さえられ限りなく0に近づき小さくなっていく数列 \right\} \)

になります。補足：{}で括ることにより数列であることを表しています

ここで\({ a }_{ n }\)に注目すると\(0\)の下界を持ち単調減少していることが確認できます。つまり０への収束がこれで証明できた事となります

実務では\(\varepsilon=\frac { 1 }{ 100000000000000000000000000000000000000000000000000000 }\)のような任意の数（勝手な数）をいきなり入れてもかまいません
無限に近い分母の数を入れても\(\left| { a }_{ n } \right|\) は \(0<\left| { a }_{ n } \right| <\varepsilon\)になります