メモ1

P63～

P58～61の理解（対称群の理解など）

資料：

• 対称群
• 頂点推移グラフ

順列の中から幾何的な図となる関係を見つけることができる。その考えの土台には対称群、置換群の考え方がベースにある

例：三次の対称群\({S}_{3}\)を考えると
\(\left| { S }_{ 3 } \right| \quad =\quad 3!\quad =\quad 3\times 2\times 1\quad =\quad 6\)

順列に対し置換群の意味を振り分けると以下になる（\(\iota\)（イオタ）を恒等置換。\(\sigma\)（シグマ）を左向きの回転。\(\tau\)（タウ）を全要素の反転と考えている）
\(123\quad =\quad \iota \\ 132\quad =\quad \tau \cdot { \sigma }\\ 213\quad =\quad \tau \cdot { \sigma }^{ 2 }\\ 231\quad =\quad \sigma \\ 312\quad =\quad { \sigma }^{ 2 }\\ 321\quad =\quad \tau \)

\({ S }_{ 3 }=\left\{ \quad \iota \quad ,\quad \tau \cdot { \sigma }\quad ,\quad \tau \cdot { \sigma }^{ 2 }\quad ,\sigma \quad ,\quad { \sigma }^{ 2 }\quad ,\quad \tau \quad \right\} \)

これを頂点推移グラフにすると以下のような幾何図になり推移や置換の関係がよく分かるようになる
（数学を知らべていて考え方が図になって行くのは不思議な感じがする）

対称群の中の置換群

テーブルの上の6皿の回転を数学的に表現した置換群R
\(R=\left\{ { \sigma }^{ k }|0\le k\le 5 \right\} =\left\{ \iota ,{ \sigma }^{ 1 },{ \sigma }^{ 2 },{ \sigma }^{ 3 },{ \sigma }^{ 4 },{ \sigma }^{ 5 } \right\} \)

P51～P57の理解

資料：イテレータ

プログラムコードで表現した方が話が早い
「プログラムの言葉」を「数学の言葉」で表しているだけ

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

- | | | | - - ! | | | ! | - | ! - | | ! | - | ! - | | ! !

using UnityEngine; using System.Collections; public class circle : MonoBehaviour { int[] X = { 1, 2, 3, 4, 5, 6, }; //番号の集合X　ここであえて視覚化しているがこれは使わない。プログラムでは0から始まる配列番号（自然数）があるからそちらを利用する char[] Y = { 'A', 'B', 'C', }; //料理の集合Y　A=シューマイ、B=棒棒鶏、C=酢豚 void Start() { //なっとくする群環体P54のプログラムコードによる再現。配列番号に合わせて1引算しています print( f(sigma(1-1)) ); print( f(sigma(2-1)) ); print( sigma(sigma(sigma(1-1))) ); //σ^3 } //σ:X→X //番号の回転関数σ（X上の置換）P53参照 private int sigma(int x) { int[] shift = { 5, 0, 1, 2, 3, 4, }; return shift[x]; } //f:X→Y //番号の集合Xから料理の集合Yへの関数　（意味や型の変換とも言える。この場合、「番号」から「テーブルに並んだ料理」へと意味が変わっている）P52参照 private char f(int x) { int[] y = { 0, 1, 1, 0, 0, 2, }; //Yの集合から回転テーブルに並んだ料理を表すABBAACにしている return Y[y[x]]; } }

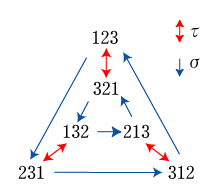
＜P56の二通りの料理の配置に関して＞

\(f:X\rightarrow Y\)　と \(g:X\rightarrow Y\)　があるとする。例えば以下のようなものを考える

\(f=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ A & A & B & B & C & C \end{pmatrix}\quad でg=f\cdot { \sigma }^{ j }としてj=2とした時、g=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ C & C & A & A & B & B \end{pmatrix}\quad となる\)

このfとgとの二項との間にテーブルの回転をモデル化した置換群Rによって同値となる事を表現する「\({ \sim }_{ R }\)」（チルダアールと読む）という数学記号を作り、適用すると「\(f{ \sim }_{ R }g\)」と表現できるようになる

\(f=g\)と書いたらfとgは同値。\(f\equiv g\quad (mod\quad m)\)と書いたらfとgはmを法として同値。\(f{ \sim }_{ R }g\)と書いたらfとgはRの置換群により同値と言えることになる

色んなグループに世の中にある、あらゆるものは分けられる。この場合、置換群によって同値類としてグループ分けされた

漸化式の性質

（自分が勝手に考えた間違っている可能性が高い記事です）

\(\sqrt { C } \)の漸化式は\({ x }_{ n+1 }=\frac { 1 }{ 2 } \left( { x }_{ n }+\frac { C }{ { x }_{ n } } \right) \)となる

この式を使い \(\sqrt { 2 } \) として \({ X }_{ n }=1\) で計算を始めると
\({ x }_{ n+1 }=\frac { 1 }{ 2 } \left( 1+\frac { 2 }{ 1 } \right) =\frac { 3 }{ 2 } =1.5\\ { x }_{ n+2 }=\frac { 1 }{ 2 } \left( \frac { 3 }{ 2 } +\frac { 2 }{ \frac { 3 }{ 2 } } \right) =\frac { 17 }{ 12 } =1.4166...\\ { x }_{ n+3 }=\frac { 1 }{ 2 } \left( \frac { 17 }{ 12 } +\frac { 2 }{ \frac { 17 }{ 12 } } \right) =\frac { 577 }{ 408 } =1.4142...\)

この数列\(\left\{ \quad{ x }_{ n+1 }\quad ,\quad { x }_{ n+2 }\quad ,\quad { x }_{ n+3 }\quad ,\quad \cdots \right\} \) は \(\left\{ \quad 1.5\quad ,\quad 1.4166...\quad ,\quad 1.4142...\quad ,\quad \cdots \quad \right\} \) となる

この漸化式の関数を経由した数列の関係を観察すると、各々の各値の関係は\({ x }_{ n+1 }>{ x }_{ n+2 }>{ x }_{ n+3 }>\cdots \)となり

\({ x }_{ n+1 }>{ x }_{ n+1 }\quad \quad \quad 反射性NG\\ { x }_{ n+1 }>{ x }_{ n+2 }\quad \rightarrow \quad { x }_{ n+2 }>{ x }_{ n+1 }\quad \quad \quad 対称性NG\\ { x }_{ n+1 }>{ x }_{ n+2 }\quad \wedge \quad { x }_{ n+2 }>{ x }_{ n+3 }\quad \rightarrow \quad { x }_{ n+1 }>{ x }_{ n+3 }\quad \quad \quad 推移性OK\)

従って同値性は持たず推移性を持つ事になる
値が回転ループすることもないし、ある具体的な値に固定化（同値化）することもない（つまり同値でなく近似値になる）。演算の順番も反射性、対称性が無いので入れ替えれない
この推移性はεδ論法によって確保されていると考えられる。\(\forall \varepsilon >0\quad (\quad \exists \delta >0\quad (\quad \forall n\in \mathbb{N}\quad (\quad n>\delta \quad \Rightarrow \quad \left| { a }_{ n }-\alpha \right| <\varepsilon \quad ))))\quad\)

また、恒等や反転にあたる\(\iota \)（イオタ）や\(\tau \)（タウ）、つまり単位元、逆元のような存在は見つけられない
このような漸化式は対称性がないのでasymptote、アシメトリー_非対称な式といえるのではないか？
グラフで見た時もεとδが0より常に大きいと考えれば輪になったり左右上下が対称になるような幾何図にはならない
（引き続き要調査）

メモ：もしパラメーターに虚数があれば輪や螺旋、渦巻になる可能性があると考えられる？

数え上げ

資料：書籍「なっとくする群環体」P59
2種の数え上げ

位相幾何学（topology）

資料：

• 位相幾何学（トポロジー）
• 資料：書籍「なっとくする群環体」P48～P49

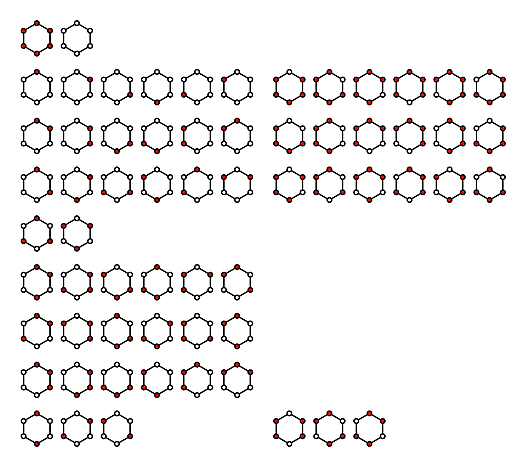
「位相幾何学として合同」な6角形の例（通常の合同とは変換の概念が異なる。rigid bodyでない変換）

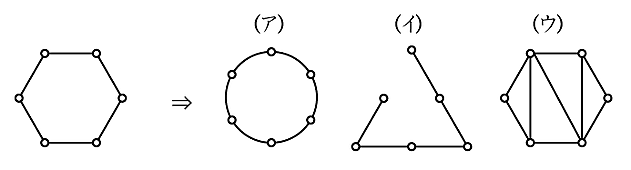
平面上の点の個数をp、それらを結ぶ線をq、線によって囲まれる領域の個数をrとすると
（ア）p=6,q=6,r=1
（イ）p=6,q=5,r=0
（ウ）p=6,q=9,r=4

これらはオイラーの定理　\( p-q+r=1\)　を満たしている。（余談：どうでもいいことだが（イ）は一本線を引くと三角形になる）
これらは変換群と呼ばれるものになるらしい

同値関係

• 資料：書籍「なっとくする群環体」P38

以下の3つの条件を満たせば同値関係として認められる

\(反射性:\quad x\sim x\\ 対称性:\quad x\sim y\quad \rightarrow \quad y\sim x\\ 推移性:\quad x\sim y\quad \wedge \quad y\sim z\quad \rightarrow \quad x\sim z\)

読み：\(\sim\) はチルダと読める。\(\wedge\) は「かつ」。\(\rightarrow\) は「ならば」
チルダは抽象化された二項の同値関係を表現するときに使われる。つまり、すぐに考えられる例では「\(=\)」や「\(\equiv \)」などがあてはまる（数学的に記号化されたもの以外の抽象化された同値関係は～で表現される）

具体例を列挙してみる

「\(\sim\) 」を「=」と考えた場合

\( x=x\quad 反射性OK\\ x=y\quad \rightarrow \quad y=x\quad 対称性OK\\ x=y\quad \wedge \quad y=z\quad \rightarrow \quad x=z\quad 推移性OK\)

つまり2項を「=」で挟んだ式、「○=△」等は○と△は同値関係であると言える

「\( \sim\) 」を「\(\equiv \)」と考えた場合

1. \(x\equiv x\quad \left( mod\quad m \right) \)
2. \(x\equiv y\quad \rightarrow \quad y\equiv x\quad \left( mod\quad m \right) \)
3. \(x\equiv y\quad \wedge \quad y\equiv z\quad \rightarrow \quad x\equiv z\quad \left( mod\quad m \right) \)

検証（以下の式の変形には資料：書籍「なっとくする群環体」の各ページにある合同の事実や定義が利用されている点に留意）

1. \(x-x=0\cdot mと変形できるので反射性OK\)
2. \(x-y=q\cdot m\quad \rightarrow \quad y-x=-q\cdot mと変形できるので対称性OK\)
3. \(x-z=(x-y)+(y-z)=q\cdot m+r\cdot m=(q+r)\cdot mなので推移性OK\)

つまり2項を「\(\equiv \)」で挟んだ式、「○\(\equiv \)△」等は○と△は同値関係であると言える

「\(\sim\) 」を「＜」と考えた場合

\(x<x\quad \quad \quad 反射性NG\\ x<y\quad \rightarrow \quad y<x\quad \quad \quad 対称性NG\\ x<y\quad \wedge \quad y<z\quad \rightarrow \quad x<z\quad \quad \quad 推移性OK\)

つまり2項を「＜」で挟んだ式、「○＜△」等は○と△は同値関係では無いと言える

「\(\sim\) 」を「\(\le\)」と考えた場合

\(x\le x\quad \quad \quad 反射性??\\ x\le y\quad \rightarrow \quad y\le x\quad \quad \quad 対称性??\\ x\le y\quad \wedge \quad y\le z\quad \rightarrow \quad x\le z\quad \quad \quad 推移性OK\)

つまり2項を「\(\le\)」で挟んだ式、「○\(\le\)△」等は○と△は？？？（TODO:要調査）