整数 
- 2以上の自然数\(\mathbb{N}\)はすべて素数(prime)と、その合成で出来ている。そして、その各々の数の合成に使う素数の構成は乗算する順番を除いて一意性を持っている
例:\(364={ 2 }^{ 2 }\times 7^{ 1 }\times 13^{ 1 }\) (4週間、7日、13ヵ月?)
- 最大公約数が1の場合、「互いに素」の関係となる
例. 5と24は互いに素。
最大公約数 gcd 、最小公倍数 lcm は素因数分解をすることで求めることが出来る。また「ユークリッドの互除法」を利用して最大公約数を求める事も出来るが元をたどった仕組み自体は素因数分解にある
例: 各素数の指数部の小さい方を掛け合わせると最大公約数に、大きい方を掛け合わせると最小公倍数になる
\(84\quad =\quad { 2 }^{ 2 }\times 3^{ 1 }\times 5^{ 0 }\times 7^{ 1 }\times 11^{ 0 }\\ 550\quad ={ \quad 2 }^{ 1 }\times 3^{ 0 }\times 5^{ 2 }\times 7^{ 0 }\times 11^{ 1 }\)
\(gcd\left( 84,50 \right) \quad =\quad { 2 }^{ 1 }\times 3^{ 0 }\times 5^{ 0 }\times 7^{ 0 }\times 11^{ 0 }\quad =\quad 2\\ lcm\left( 84,50 \right) \quad =\quad { 2 }^{ 2 }\times 3^{ 1 }\times 5^{ 2 }\times 7^{ 1 }\times 11^{ 1 }\quad =\quad 23100\)
ユークリッドの互除法は商(quotient)と余り(remainder)を交互に書き換えながら計算して余りが0になるまで計算すると求められる
(TODO)
合同式 
合同式は数を性質で分け集合に分類する事に利用できる。また非常に面白い良い性質を持っている
たとえば以下のような問題があったとする
<問題>
1000000000000002は9で割り切れるか?3では?
小さな数から合同式で考えてみる
\(365\equiv 1\quad \left( mod\quad 7 \right) \)
これは\(365-1=364\)、\(364\)は\(7\)で割り切れる。ということを合同式で表している
\(10\equiv 1\quad \left( mod\quad 9 \right) \)
これは\(10-1=9\)、\(9\)は\(9\)で割り切れる。ということを表している
\({ 10 }^{ 2 }\equiv { 1 }^{ 2 }\quad \left( mod\quad 3,9 \right) \)
これは\({10}^{2}-1=99\)、\(99\)は\(3\)や\(9\)で割り切れる。ということを表している。割り切れる数は複数ある時もある。必ず割り切れる数を全て書く必要はなく自分が表現したい事を書けばいい
合同式を自分が表現したい集合を表現する為に利用する事が大事
<問題>
1000000000000002は9で割り切れるか?3では?
これを合同式で考えると
\({ 10 }^{ 15 }+2\equiv { 1 }^{ 15 }+2\quad \left( mod\quad 9 \right) \quad \quad \Rightarrow \quad \quad 1000000000000002\equiv 3\quad (mod\quad 9)\quad \quad \Rightarrow \quad \quad 1000000000000002\equiv 0\quad (mod\quad 3)\)
のように表せる。つまり元の数から\(3\)引き算しないと\(9\)では割り切れない。3では割り切れる という事がこれで説明できる
同値類 
<問題>
\(\mathbb{Z}/\left( 5 \right) \)の同値類 \(C\left( x \right) \quad \left( 0\le x\le 4 \right) \) の乗算表を作りなさい
整数の集合\(\mathbb{Z}\)に対して5で割り切れる0~4の余りを持つ同値類の集合を作る。その集合を表すと以下になる
\(\mathbb{Z}/\left( 5 \right) \quad =\quad \left\{ C\left( 0 \right) ,C\left( 1 \right) ,C\left( 2 \right) ,C\left( 3 \right) ,C\left( 4 \right) \right\} \\ C\left( 0 \right) =\quad \left\{ 5k+0|k\in \mathbb{Z} \right\} \quad =\quad \left\{ \cdots ,-10,-5,0,5,10,15,\cdots \right\} \\ C\left( 1 \right) =\quad \left\{ 5k+1|k\in \mathbb{Z} \right\} \quad =\quad \left\{ \cdots ,-9,-4,1,6,11,16,\cdots \right\} \\ C\left( 2 \right) =\quad \left\{ 5k+2|k\in \mathbb{Z} \right\} \quad =\quad \left\{ \cdots ,-8,-3,2,7,12,17,\cdots \right\} \\ C\left( 3 \right) =\quad \left\{ 5k+3|k\in \mathbb{Z} \right\} \quad =\quad \left\{ \cdots ,-7,-2,3,8,13,18,\cdots \right\} \\ C\left( 4 \right) =\quad \left\{ 5k+4|k\in \mathbb{Z} \right\} \quad =\quad \left\{ \cdots ,-6,-1,4,9,14,19,\cdots \right\} \)
整数全体を「性質」により5つの集合に分け同値類としている。同値類を作るには3つの条件を満たす必要がある。反射性、対称性、推移性。これらを満たせば2項演算子(×とか+とかそういう演算子の事)により同値関係同士の演算が可能となる。ここでは条件はとりあえず飛ばして、乗算で同値類の計算結果の表を作ってみる
\(\mathbb{Z}/\left( 5 \right) \)での積 
| C(0) | C(1) | C(2) | C(4) | C(4) |
| C(0) | C(0) | C(0) | C(0) | C(0) | C(0) |
| C(1) | C(0) | C(1) | C(2) | C(3) | C(4) |
| C(2) | C(0) | C(2) | C(4) | C(1) | C(3) |
| C(3) | C(0) | C(3) | C(1) | C(4) | C(2) |
| C(4) | C(0) | C(4) | C(3) | C(2) | C(1) |
<例>
行C(2)、列C(3)の積を計算してみる
C(2)の集合から合同式を作る
\(2\equiv 7\quad (mod5)\)
C(3)の集合から合同式を作る
\(3\equiv 8\quad (mod5)\)
\(C(2)\times C(3)\quad =\quad 2\times 3\equiv 7\times 8\quad (mod5)\)
\(\left\{ 6,56 \right\} \in C(1)\) なので積の計算の結果はC(1)の同値類となる事がわかる
これにより整数という無限の集合を5ブロックに完璧に分ける事が出来たことになる。この5ブロック同士の二項演算の結果は、少なくとも積に関してこの中で完結する事が確認出来た
関数とは何か? 
関数には幾つか種類がある
- 物理的な働きを表す関数
- 数式で表現される関数
- 人工的に表現された関数
<具体例>
- モノが時間に従って落下する距離を表現した関数。\(y=4.9{t}^{2}\)等がある
- 抽象的な計算に利用される関数。\(y=3{x}^{2}+2x+5\)等がある
- あみだくじ、バブルソート、ハノイの塔の一手順、確率の置換の一手順等がある
<補足>
何故、あみだくじは関数か?
関数は1対1に漏れなく対応し重複がない性質を持っていれば、それは関数だといえる
以下のようなあみだくじがあるとする
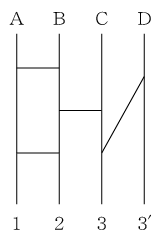
あみだくじの各経路は漏れなく1対1に物事を対応させ、交点に合流はなく、逆にたどれば元がわかる
つまり関数で表すと
f(A)=3'
f(B)=2
f(C)=1
f(D)=3
と表せる。従ってあみだくじは関数といえる。このような考え方でいろんな物事を見るとアルゴリズムのハノイの塔の一手順、確率の置換なども関数と言えてくる。数学的帰納の考え方で、その関数を入力を1づつインクリメントしながら実行していくとある性質が実現し、その数を数え上げる事でも対応する数が生まれるらしい?(たとえばこのあみだくじの入力ABCDはアルファベット順に1づつインクリメントされているとも考えられる)
あみだくじの上側の集合をX={A,B,C,D}、下側の集合をY={1,2,3,3'}とすると、あみだくじはfと表現できる
f:X→Y
このfの機能、x∈Xに対応するy∈Yは「あみだくじの図」で人工的に図形で表現される
ある一定のルールを守って、このような集合とfとの関係を作ると関数同士の演算も可能となる
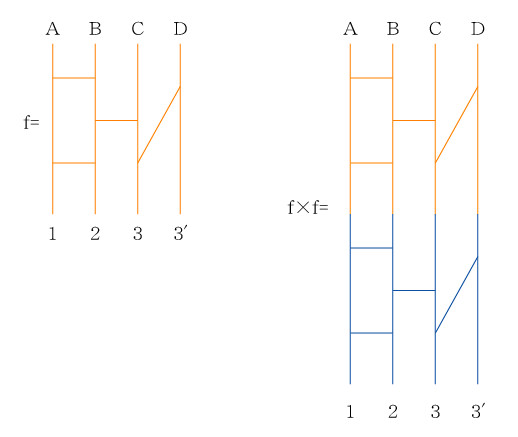
f×f(A)=3
f×f(B)=2
f×f(C)=3'
f×f(D)=1