|
ページ内コンテンツ
式木、二項演算、括弧のネスト処理
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 | - | | | | | ! - | | - | - ! | | | | | | | | | | | | | | | | | | ! | | - | ! - | | | | | - | ! | - ! - - ! | | - | | | ! | - | ! - ! | | - ! | | - ! ! | - | ! - - ! | | | - ! | - | | | | | | | ! | | | | - ! | - ! | | | ! | - ! - | | | | | | | | - ! - | - | | | | | | | | ! | - | | | ! - | | ! ! | | ! | | - | | | | | | ! | | - | | | | | | | | | | | | | ! | | - | | | | | | ! | - | ! - - ! - - ! | | - ! - | | | | | ! ! - | ! ! ! ! | |
次にルール3.の括弧の処理を考える。例えば二項結合子と左右の二項を一ブロックに考えて \(a①b\) という式があった場合、これに括弧を付けると \((a①b)\) になる。\(a①b②c\) の場合に括弧を付ける場合、 \(\left( a①\left( b②c \right) \right) \) か \(\left( \left( a①b \right) ②c \right) \) となる。このことから、二項結合子を挟んだ2項に対して左右に括弧で囲めば式を生成できる。そこで①をtrue,falseを持つフラグだと考える
①がfalseの時は
\(a①b②c③d\)
①がtrueの時は
\((a①b)②c③d\)
このルールに従って表を作ると以下のようになる
| ①②③ | ||
| 000 | a①b②c③d | |
| 001 | a①b②(c③d) | |
| 010 | a①(b②c)③d | |
| 100 | (a①b)②c③d | |
| 101 | (a①b)②(c③d) | |
| 011 | a①(b②(c③d)) | a①((b②c)③d) |
| 110 | ((a①b)②c)③d | (a①(b②c))③d |
| 111 | (a①(b)②(c)③d) |
括弧の処理順を考えると000⇔111で同値となっている。これはひとつにする。従ってabcdと①②③の中身を変化させず全部で9パターンの式を作れば括弧ありの式の状態を網羅したことになる。ここで011の括弧の生成をすると
例:"5/(3+(2*4))"
①=/
②=+
③=*
a=5
b=3
c=2
d=4
一番優先順位が低い結合子は ①=/ になる。従って式木は
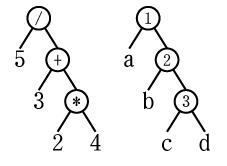
この一番優先順位が低い結合子を選ぶアルゴリズムは資料のGetOperatorPos関数にある
括弧もここでうまく処理されているので注目。もう一例
例:"(5/(3+2))*4"
一番優先順位が低い結合子は ③=* になる。従って式木は
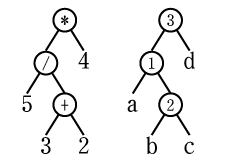
この要領で式木を生成すればいい。式木の末端程、計算優先順位は高くなるのでcalculate時は末端からトラバースして計算する
式木から数式のパターンを眺めてみる 
ここで視点を変えて式木から数式のパターンを眺めてみる。よくある式の一つを眺めてみると以下のような構成となっている(見やすさを優先して横倒しにしています)
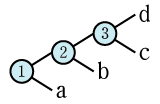
この①~③の並びを順列と考えて置換すると
①②③
①③②
②①③ ×
②③① ×
③①②
③②①
の \(3!=3\times 2\times 1=6\) パターンで全てを網羅する事ができる。そこで、この式木を実際に組んで性質をまとめてみる。まず、以下の約束事を定義する
\(①,②,③=\left\{ \times ,\div ,+,- \right\} \\ \overline { ① } ,\overline { ② } ,\overline { ③ } =\left\{ \times ,\div \right\} \\ \underline { ① } ,\underline { ② } ,\underline { ③ } =\left\{ +,- \right\} \)
二項結合演算子(この場合①~③で「×÷+-」の集合)に上線があるものは優先順位の高い演算子の集合「×÷」。下線のあるものは優先順位の低い演算子の「+-」の集合になっている。このルールに従い式木から数式を見ると以下のような分類が可能となる
式木123のパターン 
\(a①\left( b②\left( c③d \right) \right) \quad \Leftrightarrow \quad 例:\quad 1\times \left( 2\times \left( 3\times 4 \right) \right) \quad \\ a\underline { ① } b\overline { ② } \left( c③d \right) \quad \Leftrightarrow \quad 例:\quad 1+2\times \left( 3\times 4 \right) \)

式木132のパターン 
\(a\underline { ① } \left( b②c \right) \overline { ③ } d\quad \Leftrightarrow \quad 例:\quad 1+\left( 2\times 3 \right) \times 4\quad \\ a①\left( \left( b②c \right) ③d \right) \quad \Leftrightarrow \quad 例:\quad 1\times \left( \left( 2+3 \right) +4 \right) \quad \)
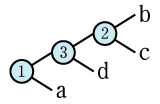
式木312のパターン 
\(a\overline { ① } \left( b②c \right) \underline { ③ } d\quad \Leftrightarrow \quad 例:\quad 1\times \left( 2\times 3 \right) +4\quad \\ \left( a①\left( b②c \right) \right) ③d\quad \Leftrightarrow \quad 例:\quad \left( 1+\left( 2+3 \right) \right) \times 4\)
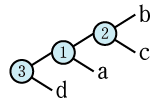
式木321のパターン 
\(\left( a①b \right) \overline { ② } c\underline { ③ } d\quad \Leftrightarrow \quad 例:\quad \left( 1\times 2 \right) \times 3+4\quad \\ \left( \left( a①b \right) ②c \right) ③d\quad \Leftrightarrow \quad 例:\quad \left( \left( 1+2 \right) +3 \right) \times 4\)
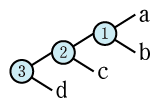
式木亜種のパターン 
\(\left( a①b \right) ②\left( c③d \right) \quad \Leftrightarrow \quad 例:\quad \left( 1+2 \right) \times \left( 3+4 \right) \\ a\overline { ① } b\underline { ② } \left( c③d \right) \quad \Leftrightarrow \quad 例:\quad 1\times 2+\left( 3\times 4 \right) \\ \left( a①b \right) \underline { ② } c\overline { ③ } d\quad \Leftrightarrow \quad 例:\quad \left( 1\times 2 \right) +3\times 4\)
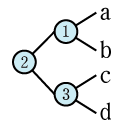
式木から見て②から始まるパターンは使えない 
式木から見て②から始まるパターンはありえない。そのことを以下で確認してみる
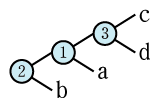
これは項同士が隣り合っていない、間に邪魔な項があり演算できない。従って式木が成立しない。231のパターンも同様である
括弧によるネストがない数式を式木として見てみる 
次に括弧によるネストがない数式を式木として見てみると以下のように上記で紹介した各パターンに重複することがわかる
\(a\overline { ① } b\overline { ② } c\overline { ③ } d\quad \Leftrightarrow \quad a\times b\times c\times d\quad \Leftrightarrow \quad 123のパターン\\ a\underline { ① } b\overline { ② } c\overline { ③ } d\quad \Leftrightarrow \quad a+b\times c\times d\quad \Leftrightarrow \quad 132のパターン\\ a\underline { ① } b\overline { ② } c\underline { ③ } d\quad \Leftrightarrow \quad a+b\times c+d\quad \Leftrightarrow \quad 312のパターン\\ a\overline { ① } b\overline { ② } c\underline { ③ } d\quad \Leftrightarrow \quad a\times b\times c+d\quad \Leftrightarrow \quad 321のパターン\\ a\overline { ① } b\underline { ② } c\underline { ③ } d\quad \Leftrightarrow \quad a\times b+c+d\quad \Leftrightarrow \quad 321のパターン\\ a\underline { ① } b\underline { ② } c\underline { ③ } d\quad \Leftrightarrow \quad a+b+c+d\quad \Leftrightarrow \quad 321のパターン\\ a\underline { ① } b\underline { ② } c\overline { ③ } d\quad \Leftrightarrow \quad a+b+c\times d\quad \Leftrightarrow \quad 亜種のパターン\\ a\overline { ① } b\underline { ② } c\overline { ③ } d\quad \Leftrightarrow \quad a\times b+c\times d\quad \Leftrightarrow \quad 亜種のパターン\)
中間まとめ 
以上の事から式木の5パターンで4項の括弧を含めた四則演算の優先順位が網羅できることが確認できる
この考えが正しいかどうか。まずブルートフォースの形式で力技で率直にアプローチしたコードと、5パターンにまでシンプル化した式木を利用したコードのふたつで検証を行い、どちらの答えも同一であれば、まず間違いはないだろうと考える。コーディングはまだ早い。もう少し考えを進めてみる
群(group)の理論で、式木の置換処理を考える 
資料:群 (数学)
数学における「群」とは「似ているものをひっくるめる」理論といえる。似ているもの同士がどこが似ているかを人に説明するのは難しい。その対象が抽象的な物であればある程難しいものだと考えられる。
![[PukiWiki] [PukiWiki]](http://unitylabo.s601.xrea.com/xoops/modules/xpwiki/image/pukiwiki.png)