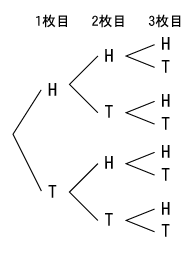
case.1
|
| パターン数 | ||
| 全て表が出たパターン | HHH | \({ _{ 3 }{ C }_{ 0 } }=1\) |
| 2枚表が出たパターン | HHT,HTH,THH | \({ _{ 3 }{ C }_{ 1 } }=\frac { 3 }{ 1 } =3\) |
| 1枚表が出たパターン | HTT,THT,TTH | \({ _{ 3 }{ C }_{ 2 } }=\frac { 3\times 2 }{ 1\times 2 } =3\) |
| 全て裏が出たパターン | TTT | \({ _{ 3 }{ C }_{ 3 } }=1\) |
となる。この全パターン数を求める式は
\(H=1,T=1として\\ { \left( 1+1 \right) }^{ 3 }\quad =\quad _{ 3 }{ C }_{ 0 }{ 1 }^{ 3 }1^{ 0 }+_{ 3 }{ C }_{ 1 }1^{ 2 }1^{ 1 }+_{ 3 }{ C }_{ 2 }1^{ 1 }1^{ 2 }+_{ 3 }{ C }_{ 3 }1^{ 0 }1^{ 3 }\\ { 2 }^{ 3 }\quad =\quad { _{ 3 }{ C }_{ 0 } }+{ _{ 3 }{ C }_{ 1 } }+{ _{ 3 }{ C }_{ 2 } }+{ _{ 3 }{ C }_{ 3 }\quad }=\quad 1+3+3+1\quad =\quad 8 \)
となる。補足として二項分布的に考えると以下になる。以下の式の各項の値がそのまま確率になっている事から、二項定理の式が絶大な効果を持っている式である事が理解できる。その力の源泉は平均の値にあり、その式自体が表面上の計算式の影に隠れている事に注目する必要がある
\(H=0.5,T=0.5として\\ { \left( 0.5+0.5 \right) }^{ 3 }\quad =\quad _{ 3 }{ C }_{ 0 }0.5^{ 3 }0.5^{ 0 }+_{ 3 }{ C }_{ 1 }0.5^{ 2 }0.5^{ 1 }+_{ 3 }{ C }_{ 2 }0.5^{ 1 }0.5^{ 2 }+_{ 3 }{ C }_{ 3 }0.5^{ 0 }0.5^{ 3 }\\ 1^{ 3 }\quad =\quad \underbrace { { _{ 3 }{ C }_{ 0 } }\frac { 1 }{ 8 } +{ _{ 3 }{ C }_{ 1 } }\frac { 1 }{ 8 } +{ _{ 3 }{ C }_{ 2 } }\frac { 1 }{ 8 } +{ _{ 3 }{ C }_{ 3 }\frac { 1 }{ 8 } \quad } }_{ ここで各項に1/2の3乗が発生している事が突出してこの公式をスゴくさせている } =\quad \frac { 1 }{ 8 } +\frac { 3 }{ 8 } +\frac { 3 }{ 8 } +\frac { 1 }{ 8 } \quad =\quad 1\)
仮にコインが歪な形をしていて表が60%、裏が40%の確率で出る場合の式は以下になる
このように有理数で考えると分りやすい
\(H=0.6=\frac { 3 }{ 5 } ,T=0.4=\frac { 2 }{ 5 } として\\ { \left( 0.6+0.4 \right) }^{ 3 }\quad =\quad _{ 3 }{ C }_{ 0 }\left( \frac { 3 }{ 5 } \right) ^{ 3 }\left( \frac { 2 }{ 5 } \right) ^{ 0 }+_{ 3 }{ C }_{ 1 }\left( \frac { 3 }{ 5 } \right) ^{ 2 }\left( \frac { 2 }{ 5 } \right) ^{ 1 }+_{ 3 }{ C }_{ 2 }\left( \frac { 3 }{ 5 } \right) ^{ 1 }\left( \frac { 2 }{ 5 } \right) ^{ 2 }+_{ 3 }{ C }_{ 3 }\left( \frac { 3 }{ 5 } \right) ^{ 0 }\left( \frac { 2 }{ 5 } \right) ^{ 3 }\\ 1^{ 3 }\quad =\quad \underbrace { { _{ 3 }{ C }_{ 0 } }\frac { 27 }{ 125 } +{ _{ 3 }{ C }_{ 1 } }\frac { 18 }{ 125 } +{ _{ 3 }{ C }_{ 2 } }\frac { 12 }{ 125 } +{ _{ 3 }{ C }_{ 3 }\frac { 8 }{ 125 } \quad } }_{ ここで各項に\frac { 1 }{ 5 } の3乗が発生している事が突出してこの公式をスゴくさせている } =\quad \frac { 27 }{ 125 } +\frac { 54 }{ 125 } +\frac { 36 }{ 125 } +\frac { 8 }{ 125 } \quad =\quad 1\)
さて、ここで問題をもう一度読み返すと
<問題:3枚のコイン投げ> アリスは五百円玉、百円玉、十円玉を1枚ずつ投げてから言った。 「少なくとも1枚は<おもて>が出ました」 この時、すべてのコインが<おもて>になっている確率はいくらか。
「少なくとも1枚は<おもて>が出ました」という事は「全て裏が出たパターン」は全体1としての内容に含めては駄目な事に気が付く
従って確率を求める式はこうなる
\(\frac { 全て表が出た }{ 全て表が出た+2枚表が出た+1枚表が出た } \quad =\quad \frac { { _{ 3 }{ C }_{ 0 } } }{ { _{ 3 }{ C }_{ 0 } }+{ _{ 3 }{ C }_{ 1 } }+{ _{ 3 }{ C }_{ 2 } } } \quad =\quad \frac { 1 }{ 1+3+3 } \quad =\quad \frac { 1 }{ 7 } \quad =\quad 14.28...\)%
このひとつの式から確率を求める計算は非常に難しい「本当に問題と数え方を理解していないと計算ができない」事がよくわかる
では、この求めた値が正当な値であるかunityを使って検証し、その正しさを体感してみる
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| - | - ! - - | | | ! | ! | - ! - | | | - | | | ! | ! | - ! - | | - | ! | ! | - ! - | | ! | - ! - | | | | | - | | ! | ! | ! | |
何度か実行してみて求めた値とシミュレーションの値が近似する事を確かめて欲しい
![[PukiWiki] [PukiWiki]](http://unitylabo.s601.xrea.com/xoops/modules/xpwiki/image/pukiwiki.png)