確率の基礎3(幾何分布の無記憶性について)
|
| 標本空間 | 起こりうる可能性、事象(部分集合)をもれ、だぶりなく網羅した集合 |
| 確率変数 | 標本空間の各事象(部分集合)から対応する実数にする関数。\(X\)と表される事が多い |
| 幾何分布 | |
| 確率分布 | 確率を得るための関数。数学では\(P()\)と表される事が多い。標本空間上の事象、又は確率変数を入力に確率1を分布させる出力機能を持っている関数 |
| 確率 | 確率質量関数\(p()\)から得られる実数(全事象の確率を足し合わせると1になる(100%になるということ)) |
| 期待値 | |
| 偏差値 |
各パラメータの関係 
確率という実数が得られるまでの一連の流れをC#と数学の視点から見て考えるとこうなる
標本空間(例:\(\overset { オメガ }{ \Omega } \)等で表される。事象(部分集合)を集めた集合)
\(Ω=\left\{ { 表、裏 } \right\} \\ Ω=\left\{ { A、B } \right\} \\ Ω={ \left\{ ピカチョウ、フシギダワ、ニセガメ、ヘトカゲ、ギャース \right\} }\\ Ω={ \left\{ ピカチョウ、ピカチョウ以外の全部 \right\} }\\ Ω=\left\{ 背の高さが120cm以上の人、背の高さが120cm以下の人 \right\} \)
この例での「\(表\)」や「\(A\)」は事象と呼ばれる部分集合となっている
↓事象(部分集合)を\(\overset { 小文字のオメガ }{ \omega } \)へ入力
確率変数(例:\(X X(ω)\) 等、大文字で表される関数)
C#で考えると、この入力の型はジェネリック(T)になっている
X(ピカチョウ)= 3
X(ニセガメ)= 6
X(表)=10回コインを投げて表が何回目で出るかの数
入力に1対1に対応した実数(C#ではintやfloatとなる)が出力される
この例では入力「ピカチョウ」に対応した離散的な数「3番」という実数を出力する関数となっている
ここは非常に重要で事象(部分集合)を連続する順序のある数に変換している
これによりこの値をヨコ軸にしたグラフが扱えるようになる(事象と確率分布の間にこのような確率変数を挟むのはこれが目的)
↓実数Xを入力
確率分布(例:Pr(X) 等、入力実数に対応した確率の実数を返す関数)
確率の値をタテ軸に、確率変数の値をヨコ軸にすると確率分布の関数グラフで事象と確率が扱えるようになる
もちろん、イプシロンデルタ論法などを利用した解析も行えるようになる。このグラフを積分すると1になる
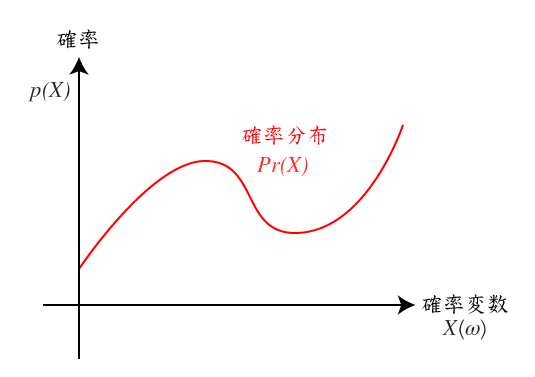
グラフに出来るという事は対象の量的な側面に注目し数値を用いて分析を行うことを意味する
このような分析を数学では「定量的に考える」と言う
また対象の状態を「不連続な性質の変化に着目して議論する際、「定性的に考える」と言う
論理記号の「ターンイー \( \exists \) (存在限量記号) はこのような議論に対し論理的に真偽を返すものとなっている
| 定性的 | 定量的 |
| 塩は舐めるとしおっからい | 水100mlに対し塩10gでしよっぱいと感じる |
ベルヌーイ試行 
幾何分布のグラフ
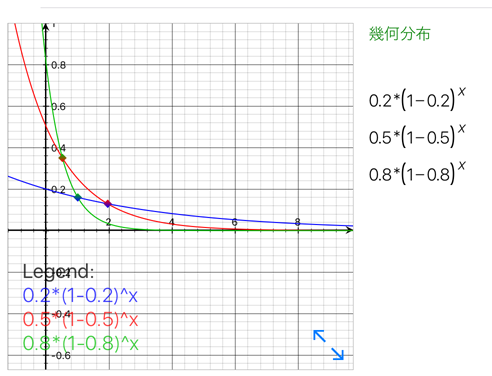
確率には以下のような公理がある
これを実際に例で表してみると・・・
関数が \(P\left( A|B \right) \) もしくは \({ P }_{ B }\left( A \right) \) と書かれていた場合、その出力は「条件付き確率」を表す
これは「ある事象B が起こるという条件下での別の事象A の確率」という意味になる
![[PukiWiki] [PukiWiki]](http://unitylabo.s601.xrea.com/xoops/modules/xpwiki/image/pukiwiki.png)