群

群１

資料：書籍「なっとくする群・環・体」より
表紙に書かれた文句を吟味して意味を考えるとunityとの相性のようなものがうかがえる

古典的な幾何学では「ずらす」とは「長さと角度を変えない平行移動回転と裏返し及びそれらの組み合わせ」でイメージとしては「動かしても形が変わらない物体（剛体：Rigidbody）」を考えている。（ゲームで例えればボーンやスケルトンの入っていないポリゴンキャラクターになるらしい）。変換：トランスフォーム（Transform）の意味を考えると合同の新しい概念が生まれる。たとえば図形をずらした時に「線の長さや形は変えてもいい」（直線を折れ線、曲線に変えてよい。切ったり繋いだり、交差させるのはNG）とすると「軟体」となり三角形は円と合同になるが線分とは合同ではない。許される変換の集合は実は”群”（変換群）となるので古典的な多くの幾何学を群論によって統一的に記述することができる。それがエルランゲン計画である。

ユークリッドの互除法関連

「なっとくする群・環・体」P28～P31。ユークリッドの互除法と一次不定方程式との関係の考えの整理。説明の具体例を考えると以下になる

\(38x+7y=1\quad \left( x,y\in \mathbb{Z} \right) \) 　の一次不定方程式を考え、これが解有りかどうかを判別するには・・・

\({ a }_{ 1 }x_{ 1 }+{ a }_{ 2 }x_{ 2 }=c\\ gcd\left( { a }_{ 1 },{ a }_{ 2 } \right) =D\\ c\equiv 0\quad \left( mod\quad D \right) を満たせば解がある\)

と考えると、まず38と7の最大公約数を求める。 \(gcd\left( 38,7 \right) =1\)
それに対して \(c=1\) なので　\(1\div 1=1\) で「解有り」となる

他にも幾つか例を考える
\(3x+9y=8\quad \left( x,y\in \mathbb{Z} \right) \)　の場合、\(gcd\left( 3,9 \right) =3\) なので\(c\)と割ると \(8\div 3=2\cdots 2\) となり割り切れないので「解無し」となる

\(42x+18y=36\quad \left( x,y\in \mathbb{Z} \right) \)の場合、\(gcd\left( 42,18 \right) =6\) なので\(c\)と割ると \(36\div 6=6\cdots 0\) となり割り切れるので「解有り」となる。これは実際にそうなのか確かめてみる

\(42x+18y=36\quad \Leftrightarrow \quad 6\left( 7x+3y \right) =36\\ s=7x+3y\\ 6s=36\quad \Leftrightarrow \quad s=6\\ 7x+3y=6\quad \Leftrightarrow \quad 3(2x+y)+x=6\\ t=2x+y\cdots ①\\ 3t+x=6\quad \Leftrightarrow \quad x=6-3t\\ ①を変形\quad y=t-2x\quad これにxを代入\quad y=t-2(6-3t)\quad \Leftrightarrow \quad y=t-12+6t\quad \Leftrightarrow \quad y=7t-12\)

従って一般解は

\(\begin{cases} x=6-3t \\ y=7t-12 \end{cases}\)　となる

パラメーター\(t\)に任意の数字を入れて計算すると\(x=\left\{ \cdots 12,9,6,3,0,-3,\cdots \right\} \quad y=\left\{ \cdots -26,-19,-12,-5,2,9,\cdots \right\} \)
これはパラメーター\(t\)に対してベクトルで表現できる

\({ a }_{ n }=\begin{pmatrix} { x }_{ n } \\ { y }_{ n } \end{pmatrix}=\begin{pmatrix} 6-3n \\ 7n-12 \end{pmatrix}=\left\{ \cdots ,\begin{pmatrix} 12 \\ -26 \end{pmatrix},\begin{pmatrix} 9 \\ -19 \end{pmatrix},\begin{pmatrix} 6 \\ -12 \end{pmatrix},\begin{pmatrix} 3 \\ -5 \end{pmatrix},\begin{pmatrix} 0 \\ 2 \end{pmatrix},\begin{pmatrix} -3 \\ 9 \end{pmatrix},\cdots \right\} \)

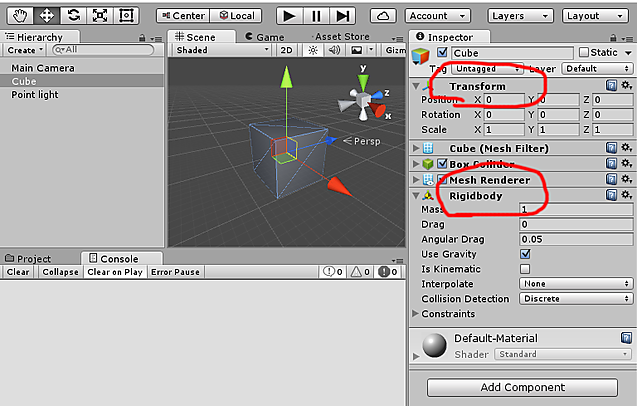
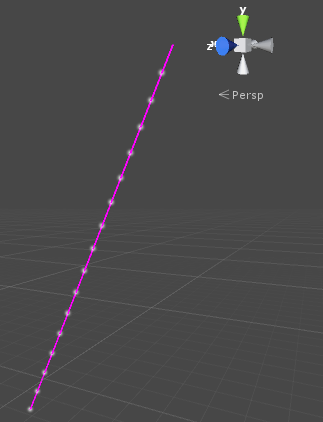
これが何故、ベクトルなのかは実際にunity上でグラフを描いてみると分かる。パーティクルとラインレンダーを利用してグラフを書いてみる。以下のコードを実行後エディタで視点を動かして確認すると直線グラフが描かれていることがわかる（このようにunityを三次元グラフを描けるツールとして利用するのも可能）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54

- | | | | | | | | | - | | | | | | | | | ! | | - | | | | | - | | | | | ! | ! | | - | ! | | - | ! | !

using UnityEngine; using System.Collections; public class Vec1 : MonoBehaviour { int work = 16; float particleSize = 3f; float lineWidth = 0.5f; LineRenderer line; ParticleSystem pe; ParticleSystem.Particle[] point; void Start() { pe = gameObject.AddComponent<ParticleSystem>(); pe.startSpeed = 0; pe.startLifetime = float.MaxValue; line = gameObject.AddComponent<LineRenderer>(); line.SetWidth(lineWidth, lineWidth); line.SetVertexCount(work+1); CreateLineAndPoint(); } void CreateLineAndPoint() { pe.Emit(work); point = new ParticleSystem.Particle[work+1]; pe.GetParticles(point); for (int n =0; n <= work; n++) { Vector3 pos = new Vector3(Xn(n), Yn(n), 0); point[n].position = pos; point[n].color = Color.white; point[n].size = particleSize; line.SetPosition(n, pos); } pe.SetParticles(point, work); } float Xn(int n) { return 6 - (3 * n); } float Yn(int n) { return (7 * n) - 12; } }

ユークリッドの互除法

ユークリッドの互除法は何度かコーディングしているが数学的帰納で書き直した

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

- | - | ! | - | ! - | - | - | ! ! !

using UnityEngine; using System.Collections; public class Alg1 : MonoBehaviour { void Start () { Gcd(44977,40589); } //ユークリッドの互除法は再帰関数で記述できる //これは関数の入力に対する置換を挟んだ数学的帰納で考えることができる　…→数学的帰納→置換関数→数学的帰納→置換関数→… private void Gcd(int m, int n) { int nn = m % n; if (nn != 0) { Gcd(n, nn); //入力m,nをn,nnに置換していると考える　つまり、これは群論で考えると準同型写像Φになる？(まだよくわかってない) } else { print("最大公約数は "+ n); } } }

ラムダ式

資料：ラムダ計算

資料中にある「ラムダ計算は1つの変換規則（変数置換）と1つの関数定義規則のみを持つ」の文に留意。ラムダ計算と群になんらかの関係性を感じる（調査の必要あり）