微積分と物理​/εδ（イプシロン、デルタ）論法

関数\(f(x)\)に対する極限の式

関数\( f(x)\)が区間\(a\le x\le b\)において連続であるものとする時
関数\( f(x)\) に対する極限の式 \(\displaystyle \lim _{ x\rightarrow a }{ f\left( x \right)=b } \) を \(\varepsilon \delta\)論法で書くと

\(\forall \varepsilon >0\quad ,\quad \exists \delta >0\quad s.t.\quad \forall x\in { \mathbb{R} },\quad 0<\left| x-a \right| <\delta \quad \Rightarrow \quad \left| f\left( x \right) -b \right| <\varepsilon \)

となる。記述には論理記号や集合論の記号が利用されている。それらの意味はウィキペディア_数学記号の表に詳しく書かれている

見慣れない記号 \(\varepsilon \delta\) とは？

\(\varepsilon\)はイプシロンと読む。\(\delta\)はデルタと読む。これは\(x\)や\(a\)のような変数や定数と同じであるが
ある質問に登場する数値を\(\varepsilon\)、返答に登場する数値を\(\delta\)とする事が慣例として意味づけられている

\(\forall \varepsilon >0\quad ,\quad \exists \delta >0\)

最初の２項。\(\forall \varepsilon >0\quad ,\quad \exists \delta >0\)　の部分は
「任意の正数\(\varepsilon\)に対して適当な正数\(\delta\)が存在する時」　となる

\(s.t.\)

次の項 \(s.t.\)　。これは～ such that ～ という意味で「右記の条件を満たすような左記は存在する」となる
ここで注意が必要なのは「この式は存在しか主張していない」という部分
つまり「ある条件下で存在する事は確実である」と仮定したら、その仮定を確かめる為の証明はまた別に必要になる
「実際に存在を証明する」という行為自体はこの式に含まれていない。それを踏まえてεδ論法は読み進めていく必要がある

手段が正しいものであるかどうかを確かめるために仮定を立てそれに従い証明を行って「考えの動作確認」をする時にこの論法は必要になる？

\(\forall x\in { \mathbb{R} }\)

その次の項 \(\forall x\in { \mathbb{R} }\)　は「任意の実数\(x\)に対し」という意味になっている

\(0<\left| x-a \right| <\delta \quad \Rightarrow \quad \left| f\left( x \right) -b \right| <\varepsilon \)

続く項は長いが一つの項になっている。\(A \Rightarrow B\) は　\(A\)の条件を満たす時、\(B\)が成立する事を意味している
\(0<\left| x-a \right| <\delta \quad \Rightarrow \quad \left| f\left( x \right) -b \right| <\varepsilon \)
この式の意味は一度展開しないと意味が分かりづらい

まず\(A\)側の式を展開してみる
\(0<\left| x-a \right| <\delta \)　この式は不等号で３項の関係を表現している。従って２項づつに分離して展開を進める
\(0<\left| x-a \right| <\delta \quad \rightarrow \quad \begin{cases} 0<\left| x-a \right| \quad \cdots ① \\ \left| x-a \right| <\delta \quad \cdots ② \end{cases}\)
次に\(x-a\)は絶対値記号 \(\left| \right|\) で囲まれているので、これを外すために場合分けして展開する。すると以下のようになる

\(①より\\ 0<x-a\quad \rightarrow \quad a<x\quad \cdots ③\\ 0<-(x-a)\quad \rightarrow \quad 0<-x+a\quad \rightarrow \quad x<a\quad \cdots ④\\ ③④より x\neq a\)

\(②より\\ x-a<\delta \quad \rightarrow \quad x<a+\delta \quad \cdots ⑤\\ -(x-a)<\delta \quad \rightarrow \quad -x+a<\delta \quad \rightarrow \quad -x<-a+\delta \quad \rightarrow \quad x>a-\delta \quad \cdots ⑥\)

\(⑤⑥より\\ a-\delta <x<a+\delta \)

まとめると\(A\)は以下になる
\(\begin{cases} x\neq a \\ a-\delta <x<a+\delta \end{cases}\)

次に\(B\)側の式を展開する
\(\left| f\left( x \right) -b \right| <\varepsilon\)

これも同じように絶対値記号を外すために場合分けして展開する

\(f\left( x \right) -b<\varepsilon \quad \rightarrow \quad f\left( x \right) <b+\varepsilon \quad \cdots ⑦\\ -\left( f\left( x \right) -b \right) <\varepsilon \quad \rightarrow \quad -f\left( x \right) +b<\varepsilon \quad \rightarrow \quad -f\left( x \right) <-b+\varepsilon \quad \rightarrow \quad f\left( x \right) >b-\varepsilon \quad \cdots ⑧\)

⑦⑧をまとめると\(B\)は \(b-\varepsilon <f\left( x \right) <b+\varepsilon \) となる

ここで\(AB\)をあわせると

\(\begin{cases} x\neq a \\ a-\delta <x<a+\delta \end{cases}\quad \Rightarrow \quad b-\varepsilon <f\left( x \right) <b+\varepsilon \)

となる

論法を俯瞰してみる

\(\forall \varepsilon >0\quad ,\quad \exists \delta >0\quad s.t.\quad \forall x\in { { R } },\quad 0<\left| x-a \right| <\delta \quad \Rightarrow \quad \left| f\left( x \right) -b \right| <\varepsilon \\ \\ 展開後\quad \quad \forall \varepsilon >0\quad ,\quad \exists \delta >0\quad s.t.\quad \forall x\in { { R } },\quad \begin{cases} x\neq a \\ a-\delta <x<a+\delta \end{cases}\quad \Rightarrow \quad b-\varepsilon <f\left( x \right) <b+\varepsilon \)

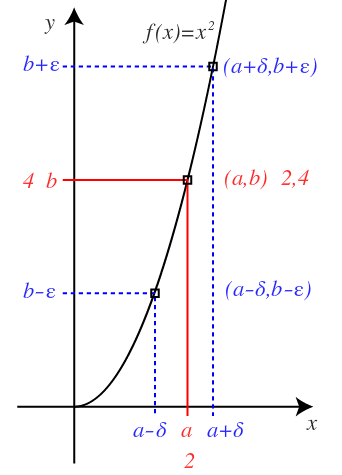
論法をunityで検証する

俯瞰して眺めるとεδ論法は日本語に翻訳でき、またunityで扱うC#へと翻訳出来る
この際、数学者はこの論法を考えの検証に利用するが、プログラマーはコードにして答えを求めるための道具にする事が出来る

つまり、\(\displaystyle \lim _{ x\rightarrow a }{ f\left( x \right)=b }\)　を処理する関数が作成できる。実際にコードにしてみる

• Prev
• Next
• 微積分と物理