<画像をクリックすると拡大表示できます>
放物線上に自由に2点を取りその点を結んだ線と放物線で囲まれた領域を三角形で取りつくして面積を求める。このような計算技術は「アルキメデスの取り尽くし法」と呼ばれています
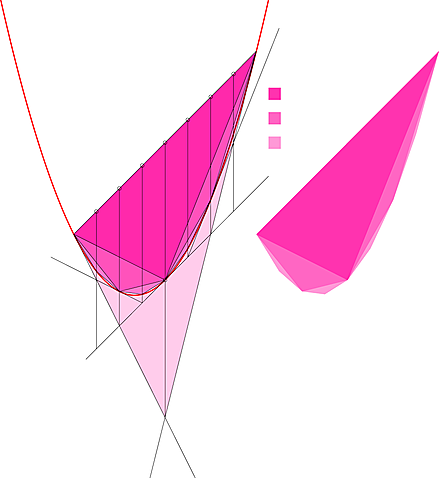
ここではドロー系のソフト(アドビ:イラストレータ)等を実際に利用しながら放物線の面積を求める一連の計算、数学的性質を検証します。ドロー系のアプリを利用する事により「二乗が生み出す驚くような数学的な整合性」も製図時のポイントスナップ機能から手と目で感じて理解できると思います(これがドロー系ソフトを使って幾何図を作図する理由です)
放物線の描画 
では実際に作画と計算を始めます。まず重要な放物線から…
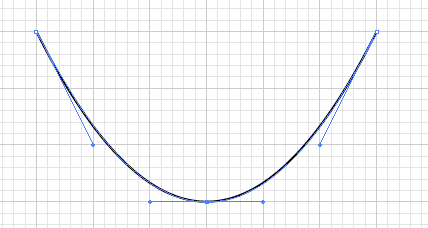
放物線はベジェ曲線でも描けます。下記、図のようにベジェ曲線を描き、縦に3倍拡大すれば正確な放物線になります。この放物線を山の頂点を基点にグリッドの(0,0)位置に配置します(画面にグリッド表示して自分で勝手に決めた位置を(0,0)とする)
これが \(y=f(x)={x}^{2}\) です
放物線上の2点接線の描画 
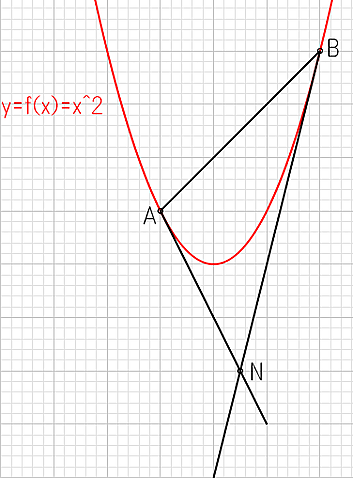
次に自由な放物線上の2点を決めます。ここでは作例として\(A\)点(-1,1)、\(B\)点(2,4)にしています。これは放物線の関数\(y=f(x)={x}^{2}\)のグラフ上の点という条件に合致しています(放物線上の点を\(P\)点とした時、\(x\)を\(\alpha\)とすると座標は\(P\left( \alpha ,{ \alpha }^{ 2 } \right) \)となる)
\(A\)点の接線から描画します。放物線の接線は導関数で計算して出します。\(A\)の位置を(-1,1)とした場合、接線の傾きは導関数\(f'(x)=2x\)なので、\(f'(-1)=2\times-1=-2\)となります。傾きは\(-2\)ということなので\(x\)が\(1\)進んだら\(y\)は\(-2\)下に進む直線で\(A\)地点の接線は表現できます。グリッドを利用してこの斜めの線を描画して(-1,1)の位置に配置してください
次に点\(B\)を作画します。\(B\)の位置は(2,4)なので、接線の傾きは\(f'(2)=2\times2=4\)となります。傾きは\(4\)ということなので\(x\)が\(1\)進んだら\(y\)は\(4\)上に進む直線で\(B\)地点の接線は表現できます。グリッドを利用してこの斜めの線を描画して(2,4)の位置に配置してください
そして、この接線を傾きをそのまま、伸ばしたいので、それを線幅はロックしたままA点の接線なら(-1,1)の位置から適当な大きさに等拡大します。\(B\)点も同様に大きくして交わらせます。これで接線の交点が出来ました。この交点を\(N\)点とします。それに加えA点とB点を結ぶ線を描きます。二つの放物線上の2点の接線と2点を結ぶ線で三角形が一つできました
以降メモ 
この要領で「虚数の情緒」P442~447までの流れをイラストレーターと手計算で追いかける。実際に手作業でイラストレータで作図すると恐ろしく頂点の位置の辻褄が合う
P448~P449は等比数列の総和の公式を別の側面から眺め説明している
<補足>
最新のイラストレーターで機能の名前が変わっている可能性があるのですが「オブジェクト -> パス -> アンカーポイントの追加」機能は便利です
これを使うと"均等な間隔"でアンカーポイントを追加できます。作図に利用してください

この線分の間隔を数学的に数列で表すなら\(\left\{ 1,\frac { 1 }{ 2 } ,\frac { 1 }{ { 2 }^{ 2 } } ,\frac { 1 }{ { 2 }^{ 3 } } ,\frac { 1 }{ { 2 }^{ 4 } } ,\cdots \right\} =\left\{ 1,{ 2 }^{ -1 },{ 2 }^{ -2 },{ 2 }^{ -3 },{ 2 }^{ -4 },\cdots \right\} \)となる
P499で式の変形が難しかったところ 
\( { k }_{ n }=\frac { 4 }{ 3 } -\frac { 1 }{ 3 } \times \frac { 1 }{ { 4 }^{ n } } \\ \rightarrow 3{ k }_{ n }=3\times \left( \frac { 4 }{ 3 } -\frac { 1 }{ 3 } \times \frac { 1 }{ { 4 }^{ n } } \right) \\ \rightarrow 3{ k }_{ n }=4-\frac { 1 }{ { 4 }^{ n } } \\ \rightarrow \frac { 1 }{ 4 } 3{ k }_{ n }=\frac { 1 }{ 4 } \left( 4-\frac { 1 }{ { 4 }^{ n } } \right) \\ \rightarrow \frac { 3 }{ 4 } { k }_{ n }=1-\frac { 1 }{ { 4 }^{ n+1 } } \\ \rightarrow { k }_{ n }=\frac { 4 }{ 3 } \left( 1-\frac { 1 }{ { 4 }^{ n+1 } } \right) \)
その内容の意味 
ここでP448の\({ S }_{ n }\)を等比数列の総和の公式\(\displaystyle \frac { { a }_{ 1 }\left( 1-{ r }^{ n } \right) }{ 1-r } \)に当てはめ考えると…
\(\displaystyle { k }_{ n }=\left\{ 1+\frac { 1 }{ 4 } +\frac { 1 }{ { 4 }^{ 2 } } +\cdots +\frac { 1 }{ { 4 }^{ n } } \right\} \)
\(\displaystyle r=\frac { 1 }{ 4 } としてみると\)
\(\displaystyle \left( 1-\frac { 1 }{ 4 } \right) { k }_{ n\quad }=\quad \left\{ 1+\frac { 1 }{ 4 } +\frac { 1 }{ { 4 }^{ 2 } } +\cdots +\frac { 1 }{ { 4 }^{ n } } \right\} -\left\{ \frac { 1 }{ 4 } +\frac { 1 }{ { 4 }^{ 2 } } +\cdots +\frac { 1 }{ { 4 }^{ n } } +\frac { 1 }{ { 4 }^{ n+1 } } \right\} \quad =\quad 1-\frac { 1 }{ { 4 }^{ n+1 } } \)
\(\displaystyle \rightarrow \quad { k }_{ n\quad }=\frac { 1-\frac { 1 }{ { 4 }^{ n+1 } } }{ 1-\frac { 1 }{ 4 } } \)
結果的に本と同じような式となる
\(\displaystyle \frac { s_{ 0 }\left( 1-\frac { 1 }{ { 4 }^{ n+1 } } \right) }{ 1-\frac { 1 }{ 4 } } \quad =\quad \frac { s_{ 0 }\left( 1-\frac { 1 }{ { 4 }^{ n+1 } } \right) \times 4 }{ \left( 1-\frac { 1 }{ 4 } \right) \times 4 } \quad =\quad \frac { 4s_{ 0 }\left( 1-\frac { 1 }{ { 4 }^{ n+1 } } \right) }{ 4-1 } \quad =\quad \frac { 4 }{ 3 } \left( 1-\frac { 1 }{ { 4 }^{ n+1 } } \right) s_{ 0 }\)
memo:
放物線をベジェ曲線で描くその数学的仕組み、整合性を後で調べる
P450~452は\(\varepsilon \delta\)論法を使わずにアルキメデスの原則と二段階帰謬を使って収束を証明している
アルキメデスの原則を細かく分解し証明したものが\(\varepsilon \delta\)論法の
\(\forall \varepsilon >0\quad (\quad \exists \delta >0\quad (\quad \forall n\in \mathbb{N}\quad (\quad n>\delta \quad \Rightarrow \quad \left| { a }_{ n }-\alpha \right| <\varepsilon \quad ))))\quad \)
と\(\displaystyle \lim _{ n\rightarrow \infty }{ \frac { 1 }{ n } } =\alpha \) 、「デデキント切断による実数の定義」となる
資料:
微積分と物理/イプシロンデルタ論法の機能考察
微積分と物理/実数の定義
最終的に、この放物線の中にある三角形の面積の扱いが重要になってくる点に注目
つまり、この三角形の合同と相似を利用すれば三角関数と対数計算が連携して機能するような事が可能となるのが予想できる
いったいどのようにすれば、繋がるのだろうか。これはこの本の後半オイラーの公式の項で説明されているらしい