基本
|
| 例 | ||
| トートロジー | リテラルがどんな真理値をとっても1となる式 | \(A\rightarrow A\) , \(A\vee \neg A\)等 |
| 事実 | リテラルがどんな真理値をとっても0か1となる式 | \(A\rightarrow B\)等 |
| 矛盾 | リテラルがどんな真理値をとっても0となる式 | \(\neg A\rightarrow A\)等 |
標準形 
連言標準形の例
\((\neg A\vee B\vee C)\wedge (D\vee \neg E\vee F)\)
選言標準形の例
\((\neg A\wedge B\wedge C)\vee (D\wedge \neg E\wedge F)\)
同値変形 
比較的、最初によく使う事になりそうなものを書くと以下になる。「ならば」や「双条件」等を選言標準形や連言標準形に変えていると言える
- \(A\rightarrow B\) は \(\neg A\vee B\) と同じ真理値になる
- \(A\leftrightarrow B\) は \((A\rightarrow B)\wedge (B\rightarrow A)\) と同じ真理値になる
このような同値変形は沢山あり、論理学を調べると憶えておくと便利なものが幾つも出てくる
述語論理 
論理式に含まれる変数を量化できる。議論領域の個体の量を指定する
はっきりと列挙できない(場合によってはノートに書ききれないぐらい沢山出てくる)対象に対して論理的に考えたい場合に使う
数学特有の言い回しで自然言語の「任意の」という言葉には注意が必要。これは「for all」なので「全ての~は」「あらゆる~は」という意味になっている
??? 
論理で使われる記号に割り当てられた自然言語は、日常的に使う意味と必ずしも合致しているとは言えない(たとえば、「ならば」等は直観的感覚で使われている日本語のならばの意味とは少し違ったりする)。その意味は真理値表で表したものが一番正確と言える。(個人的にはC#等のコンピュータ言語で利用される数学記号を使った判定式などの方がより判りやすいと思っている)。また選言標準形に直したものや連言標準形に変換したものの方がより直観的にわかりやすい場合がある
命題定数
命題変数
<極限を理解するためのキーワード、ロードマップ>
- 論理学
- 距離関数(絶対値が誘導する距離関数)イプシロンデルタ論法の一般性はこれで確保されている
- 無限
- 数学的帰納(極限の収束に至る理由。イプシロンデルタの漸化式的行動はこれを使ってる)
- 上限、下限、上界、下界、マックス、ミン
- デデキント切断
- 無限等比級数の収束(ゼノンのアキレスと亀)
- 無限小(アルキメデスの積分)
- 数学的帰納(微積分が数学的帰納の「性質」を利用している為、極限が利用できる)
- 解析という考え方、連続、一様連続、開区間、閉区間(グラフを区間で分けて性質を探る事)
\( \displaystyle \lim _{ n\rightarrow \infty }{ \frac { 1 }{ n } } =\alpha\) の極限
\( ( \forall \varepsilon >0\quad (\quad \exists \delta >0\quad (\quad \forall n\in { \mathbb{N} }\quad (\quad n>\delta \quad \Rightarrow \quad \left| \frac { 1 }{ n } -\alpha \right| <\varepsilon \quad ) ) ) ) \)
極限1/nの\(\alpha\)への収束を論理で主張、\(\delta\)の存在を問うている。以下の図のように\(\delta\)の存在を確認し、存在量化子が1になることで、この主張は真になる
(以下の図は絶対値による挟み撃ち、距離の考えを抜かしてシンプルにわかりやすく説明したものであり「関数側が1/nでnは自然数」であると負の状態を前提としない決め撃ちだから間違っていない図となっている)
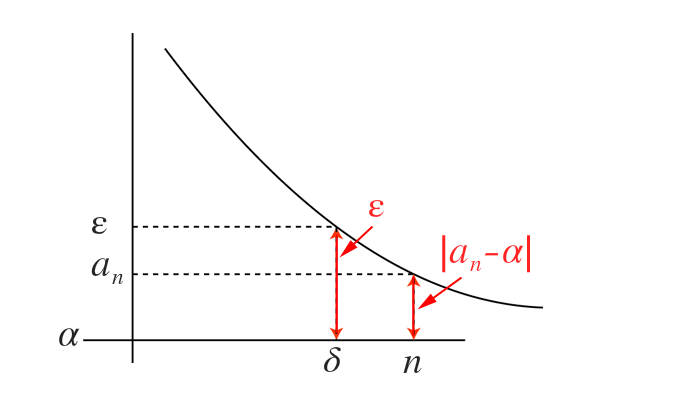
しかし、どんな関数でも対応できるイプシロンデルタ論法そのものに対して考えの抜けがある状態。数列の関数が負の場合を考えきれていない
絶対値をしっかり理解していないと、ここで終わってしまう。-1/nの極限という状態も考えてみるべきだ
\(\varepsilon\)は符号なしの距離を表した値であり、論理式の \(\left| { a }_{ n }-\alpha \right| <\varepsilon\) の部分が距離関数になっている
また同時に一様連続による「この論理が有効な区間」に対する考えも抜けている
![[PukiWiki] [PukiWiki]](http://unitylabo.s601.xrea.com/xoops/modules/xpwiki/image/pukiwiki.png)