確率と統計​/二項分布の追加検証

二項分布の追加検証

資料：数学ガール　乱択アルゴリズムP162

二項分布の動きを細かく見てみる。二項分布の定義は以下になる

\({ P }_{ n }\left( k \right) =\left( \begin{matrix} n \\ k \end{matrix} \right) { p }^{ k }{ q }^{ n-k }\)

caseA

表が出る確率50% (0.5)で裏が出る確率50% (0.5)のコインを\(n=3\)回投げる
表が\(k=2\)回出る確率\({ P }_{ 3 }\left( 2 \right) \)を求めよ

\({ P }_{ 3 }\left( 2 \right) =\left( \begin{matrix} 3 \\ 2 \end{matrix} \right) { \cdot (0.5) }^{ 2 }\cdot (0.5)^{ 3-2 }\\ =3{ \quad \cdot \quad 0.5 }^{ 2 }\quad \cdot \quad 0.5\\ =0.375\quad \Rightarrow \quad 37.5\% \)

この図はコインの出る可能性を樹形図として表したもので、表が２回、裏が１回出るときの経路が３本ある事が分かる図となっている
二項分布の定義内にあるコンビネーションの計算式はこの３本の経路であることが分かる

各経路の確率は0.5の3乗であり、これら３本が足し算されている（確率の和）
次に式を少しだけ難しくしてみる

caseB

表が出る確率60% (0.6)で裏が出る確率40% (0.4)のコインを\(n=3\)回投げる
表が\(k=2\)回出る確率\({ P }_{ 3 }\left( 2 \right) \)を求めよ
\({ P }_{ 3 }\left( 2 \right) =\left( \begin{matrix} 3 \\ 2 \end{matrix} \right) { \cdot (0.6) }^{ 2 }\cdot (0.4)^{ 3-2 }\\ =3{ \quad \cdot \quad 0.6 }^{ 2 }\quad \cdot \quad 0.4\\ =0.432\quad \Rightarrow \quad 43.2\%\)

図を見ればわかるが、３本の経路それぞれが順番は変わるが「表２回裏１回の確率の掛け算」になっている。経路数はコンビネーションの３本

上の経路から
\(表0.6\times 表0.6\times 裏0.4\\ 表0.6\times 裏0.4\times 表0.6\\ 裏0.4\times 表0.6\times 表0.6\)
各経路の確率は0.6の2乗×0.4の１乗であり、これら３本が足し算されている（確率の和）　美しい・・・

次に確率変数の期待値を見てみる

caseC

ここのベルヌーイ確率変数を成立させている考え方はとても重要なので「考え方を身につける必要がある」

参考資料1：資料：数学ガール　乱択アルゴリズムP155～182
参考資料2：ベルヌーイ過程

表が出る確率60% (0.6)で裏が出る確率40% (0.4)のコインを\(n=3\)回投げる
このとき、表が出る回数の期待値を求めよ

表が出る回数を確率変数\(X\)として\(n=3\)の場合について\(X\)の期待値を求める。順番に解決していく。まず標本空間から考える
コインを３回投げた時の「表が出る現象」に注目し起こりうる全事象を網羅した標本空間\(\ \Omega \)は以下になる

\(\Omega =\left\{ \quad { \omega }_{ 0 }=三回投げて表が0回出る\quad ,\quad { \omega }_{ 1 }=三回投げて表が1回出る\quad ,\quad { \omega }_{ 2 }=三回投げて表が2回出る\quad ,\quad { \omega }_{ 3 }=三回投げて表が3回出る\quad \right\} \)

この標本空間を定量的に考え解析しやすい形にする。「三回投げた時の表が出る回数」を量と考え、確率変数\(X\left( \omega \right) \)の関数に対応させる。その実数の数列は

\(X=\left\{ \quad { c }_{ 0 }=0\quad , \quad { c }_{ 1 }=1\quad ,\quad { c }_{ 2 }=2\quad ,\quad { c }_{ 3 }=3\quad \right\} \) となる。これは標本空間\(\ \Omega \)を対応させたものであるので全事象を網羅している

ここで例として\({c}_{2}\)が、どのような考えで\(2\)となったかを確認してみる
これは独立試行のコインを３回投げて表が出れば真_成功（１）、裏が出れば偽_失敗（０）として
その回数を数え上げ足し合わせた数と言える。つまり

上記のように計算され\(2\)という数字が算出されている。このような命題に対する真偽を\(1\)と\(0\)で、あらわし数え上げる変数を「インディケータ変数」と呼び、
ある事象が起きるかどうか\(1\)か\(0\)かで定まる確率計算と共に合わせ数え上げたものを「ベルヌーイ確率変数」と呼ぶ

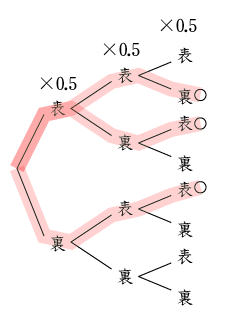
ベルヌーイ確率変数に対応する確率分布関数は、樹形図における該当する事象の樹の本数と各経路の確率が掛け合わされて、その事象の確率が算出される必要がある
よってベルヌーイ確率変数に対応する確率分布は二項分布となる

二項分布の定義は　\({ P }_{ n }\left( k \right) =\left( \begin{matrix} n \\ k \end{matrix} \right) { p }^{ k }{ q }^{ n-k }\) 　である。右辺のコンビネーション計算が樹形図の樹の数を数え上げている。それにつづく右側が確率となっている
これはcaseAやcaseBを見てもらえば何が起こっているかわかるだろう

ここで一例として\({c}_{2}\)の確率を求める計算をこれに当てはめてみると・・・

• 二項分布関数　\(P\)
• 試行回数　\(n=3\)
• 表が出る回数　\(k=2\)
• 表が出る確率　\(p=\frac { 3 }{ 5 } \)
• 裏が出る確率　\(q=\frac { 2 }{ 5 } \)

となる。そして、この確率に対し、ベルヌーイ確率変数を掛け合わせると、その事象の期待値\(E\left[ { c }_{ k } \right] \)が算出できる

\(E\left[ { c }_{ k } \right] ={ c }_{ k }\cdot \left( \begin{matrix} n \\ k \end{matrix} \right) { p }^{ k }{ q }^{ n-k }\\ \\ E\left[ { c }_{ 2 } \right] \quad =\quad 2\cdot \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) { \left( \frac { 3 }{ 5 } \right) }^{ 2 }{ \left( \frac { 2 }{ 5 } \right) }^{ 3-2 }\quad =\quad 2\cdot 3\cdot \left( \frac { 18 }{ 125 } \right) \quad =\frac { 108 }{ 125 } \)

これで確率変数\(X\)の\({c}_{2}\)の期待値が求められたことが判る。他の事象\({c}_{0}\)や\({c}_{1}\)、\({c}_{3}\)も同様の仕組みで求めることができる
これを「期待値の和」の性質を利用してシグマの式でまとめ上げたものが

\(\displaystyle E\left[ X \right] =\sum _{ k=0 }^{ n }{ { c }_{ k } } \cdot \left( \begin{matrix} n \\ k \end{matrix} \right) { p }^{ k }{ q }^{ n-k }\)　となっている

この式を利用して問題を解いてみる

\(\displaystyle E\left[ X \right] \quad =\quad 0\cdot \left( \begin{matrix} 3 \\ 0 \end{matrix} \right) { \left( \frac { 3 }{ 5 } \right) }^{ 0 }{ \left( \frac { 2 }{ 5 } \right) }^{ 3-0 }\quad +\quad 1\cdot \left( \begin{matrix} 3 \\ 1 \end{matrix} \right) { \left( \frac { 3 }{ 5 } \right) }^{ 1 }{ \left( \frac { 2 }{ 5 } \right) }^{ 3-1 }\quad +\quad 2\cdot \left( \begin{matrix} 3 \\ 2 \end{matrix} \right) { \left( \frac { 3 }{ 5 } \right) }^{ 2 }{ \left( \frac { 2 }{ 5 } \right) }^{ 3-2 }\quad +\quad 3\cdot \left( \begin{matrix} 3 \\ 3 \end{matrix} \right) { \left( \frac { 3 }{ 5 } \right) }^{ 3 }{ \left( \frac { 2 }{ 5 } \right) }^{ 3-3 }\\ \quad \quad \quad \quad \quad =\quad 0\cdot 1\cdot 1\cdot { \left( \frac { 2 }{ 5 } \right) }^{ 3 }\quad +\quad 1\cdot 3\cdot { \left( \frac { 3 }{ 5 } \right) }{ \left( \frac { 2 }{ 5 } \right) }^{ 2 }\quad +\quad 2\cdot 3\cdot { \left( \frac { 3 }{ 5 } \right) }^{ 2 }{ \left( \frac { 2 }{ 5 } \right) }\quad +\quad 3\cdot 1\cdot { \left( \frac { 3 }{ 5 } \right) }^{ 3 }\cdot 1\\ \quad \quad \quad \quad \quad =\quad 0\quad +\quad 3\cdot \frac { 12 }{ 125 } \quad +\quad 6\cdot \frac { 18 }{ 125 } \quad +\quad 3\cdot \frac { 27 }{ 125 } \\ \quad \quad \quad \quad \quad =\quad 0\quad +\quad \frac { 36 }{ 125 } \quad +\quad \frac { 108 }{ 125 } \quad +\quad \frac { 81 }{ 125 } \\ \quad \quad \quad \quad \quad =\quad \frac { 225 }{ 125 } \\ \quad \quad \quad \quad \quad =\quad 1.8\)

これは\(P=0.6\)で\(3p\)と同じ答えと言える。資料：数学ガール_乱択アルゴリズムP169の答えと同一であり\(E\left[ X \right] =np\)でこの問いには答えられることを意味している

• Prev
• Next
• 確率と統計