|
メモ 期待値の和
|
| 出目 | ⚀=1 | ⚁=2 | ⚂=3 | ⚃=4 | ⚄=5 | ⚅=6 |
| 確率 | \(\frac { 1 }{ 6 } \) | \(\frac { 1 }{ 6 } \) | \(\frac { 1 }{ 6 } \) | \(\frac { 1 }{ 6 } \) | \(\frac { 1 }{ 6 } \) | \(\frac { 1 }{ 6 } \) |
6面ダイスを一回振った時の出目の平均合計 = 6面ダイスを一回振った時の出目の期待値 = \(1\times \frac { 1 }{ 6 } +2\times \frac { 1 }{ 6 } +3\times \frac { 1 }{ 6 } +4\times \frac { 1 }{ 6 } +5\times \frac { 1 }{ 6 } +6\times \frac { 1 }{ 6 } =3.5\)
シグマで書き直すとこうなる
\(\displaystyle E\left( { X }_{ 1 } \right) \quad =\quad \sum _{ k=1 }^{ 6 }{ k } \cdot \frac { 1 }{ 6 } \quad =\quad \frac { 1+2+3+4+5+6 }{ 6 } \quad =\quad 3.5\)
ダイスを振るという行為自体が独立試行性を持っているので単純に10回加算すれば期待値の和として答えが出てくる
\(E\left[ X \right] \quad =\quad E\left( { X }_{ 1 } \right) +E\left( { X }_{ 2 } \right) +E\left( { X }_{ 3 } \right) +\cdots +E\left( { X }_{ 9 } \right) +E\left( { X }_{ 10 } \right) \)
\(3.5\times 10=35\)
unityで実際に検証してみる
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| - | - ! - | ! | | - | | | | - | | - | ! | ! | ! | | - | ! ! | |
ランダム関数で6面ダイスを10回振り合計する。それを10万回サンプリングし平均を求める
結果、計算通り\(35\)周辺の値に収束する。以上により「すごろくマップの35マス目にゴールを設定すれば希望通りのゲームバランスになる」
<考察>
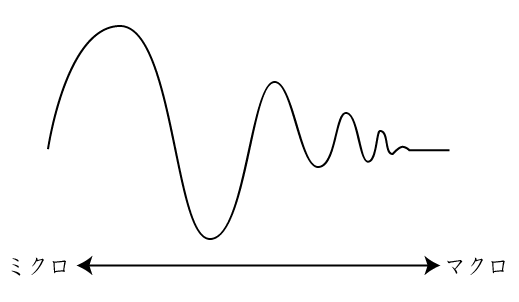
10万回オーダーのマクロの視点で見るのと数回オーダーのミクロで見るのと結果が違うのは確率に起因していると考えられる
試行回数を増やして行くとランダムの振り幅は減少しある一点の値に収束していく
イメージ図
<宿題>
- この収束していく様子は関数のイプシロンデルタ論法で説明出来るのだろうか??
![[PukiWiki] [PukiWiki]](http://unitylabo.s601.xrea.com/xoops/modules/xpwiki/image/pukiwiki.png)