確率と統計​/期待値と鳩の巣原理

期待値と鳩の巣原理

資料：幾何分布の期待値の導出

＜問題＞
長縄跳び、1000回に1回しか失敗しない人を、30人集めてやったら、飛べる回数の期待値は、どれぐらいなんだろう。

この問題のディテールを自分なりに確認してみる

準備段階

順番に考えていく。確率は「起こり得る全体の中で希望するものの割合である」。従って
1000回に1回しか失敗しない人の「縄跳びを一回跳ぶ事に失敗する確率」は\(\frac { 1 }{ 1000 } =0.001\)。成功する確率は\(\frac { 999 }{ 1000 } =0.999\)となる
ここで思考実験として「３人で縄跳びを一回跳ぶ」事を考える。

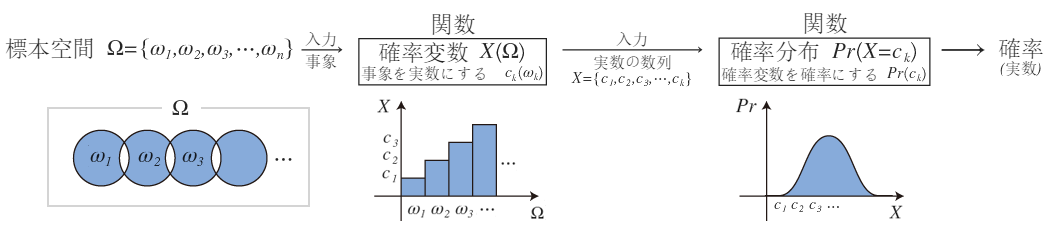
確率（正規化された量：実数）を論じるとき、事象で構成された標本空間（集合）\(\Omega\)と、それに対応する確率分布（関数）\(Pr\)が必要となる
この問題に当てはまる標本空間を考えると・・・

\(標本空間\Omega =\left\{ { \omega }_{ 1 }=一人が縄跳びを跳んで成功する,{ \omega }_{ 2 }=一人が縄跳びを跳んで失敗する \right\} \)
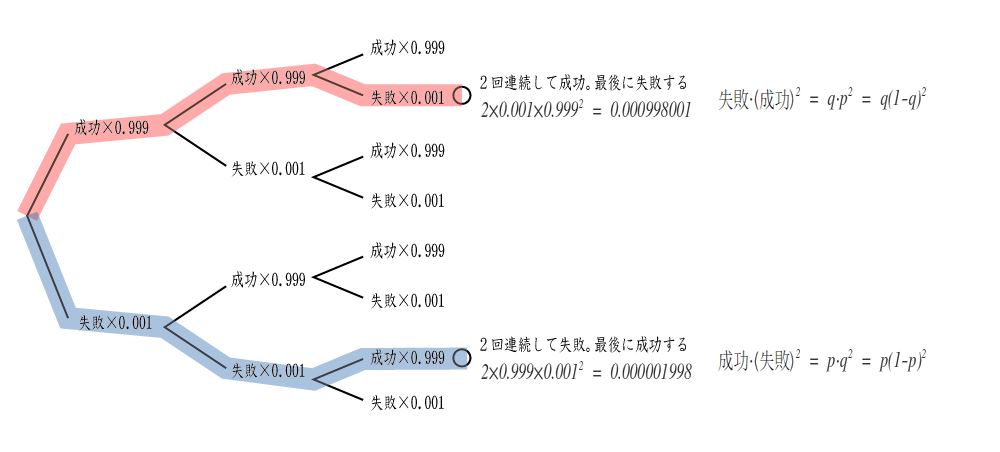
となる、この標本空間から「３人で縄跳びを一回跳ぶ」樹形図を作成する

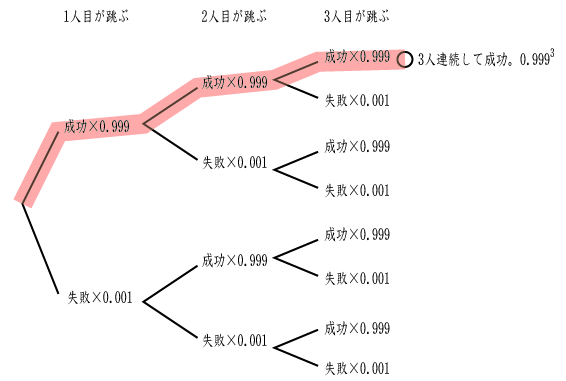
樹形図の1分岐目が1人目が跳んだ事象を表し、2分岐目が2人目が跳んだ事象を表している
このような事象の成否によって無記憶性を持って分岐する確率分布を二項分布と呼ぶ

＜二項分布の定義＞
\({ P }_{ n }\left( k \right) =\left( \begin{matrix} n \\ k \end{matrix} \right) { p }^{ k }{ q }^{ n-k }\)

この樹形図で「３人で縄跳びを一回跳ぶ事に成功する事象」を探す。これは一番上のルートであることが分かる
これを二項分布に当てはめると一番上のルートを表す式は \(p=0.999,q=0.001,n=3,k=3\) となり
\({ P }_{ 3 }\left( 3 \right) \quad =\quad \left( \begin{matrix} 3 \\ 3 \end{matrix} \right) { \cdot 0.999 }^{ 3 }\cdot 0.001^{ 3-3 }\quad =\quad 1{ \cdot 0.999 }^{ 3 }\cdot 1\quad =\quad { 0.999 }^{ 3 }\)
従ってその確率は\(\\ { 0.999 }^{ 3 }=0.997002999...\)となる。これが30人いる場合は\({ 0.999 }^{ 30 }=0.970430967...\)となる事が分かる

では、「３人で縄跳びを一回跳ぶ事に失敗する事象」の確率はどうなるだろうか。この事象を論理で考えると

３人で縄跳びを一回跳ぶ事に失敗した　⇒(ならば)　ひとりでも縄に引っかかっている　となる

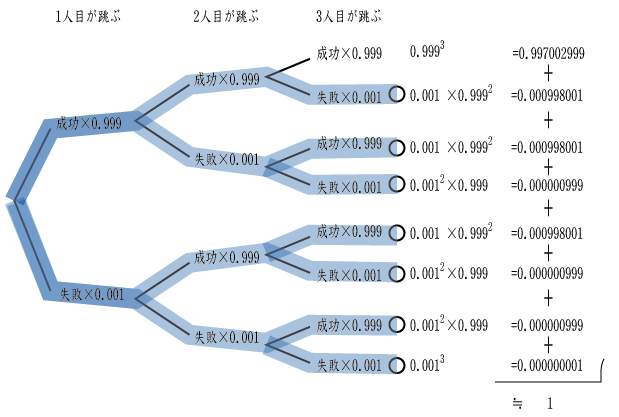
ここでやりがちな間違いとは\({ 0.001 }^{ 30 }\)を失敗の確率と考えてしまう事である。この場合を樹形図で確認すると、一番下のルートのみを計算したことになり「ひとりでも縄に引っかかっている」という必要条件を満たさなくなる。では下図の青ルートを計算するとして30人になった場合の事を考えると、それぞれ計算し各ルートを足し合わせる事になるので、この計算はとても大変な事だと解ってくる（この樹形図は右に伸びていくほど分岐が増えていく）

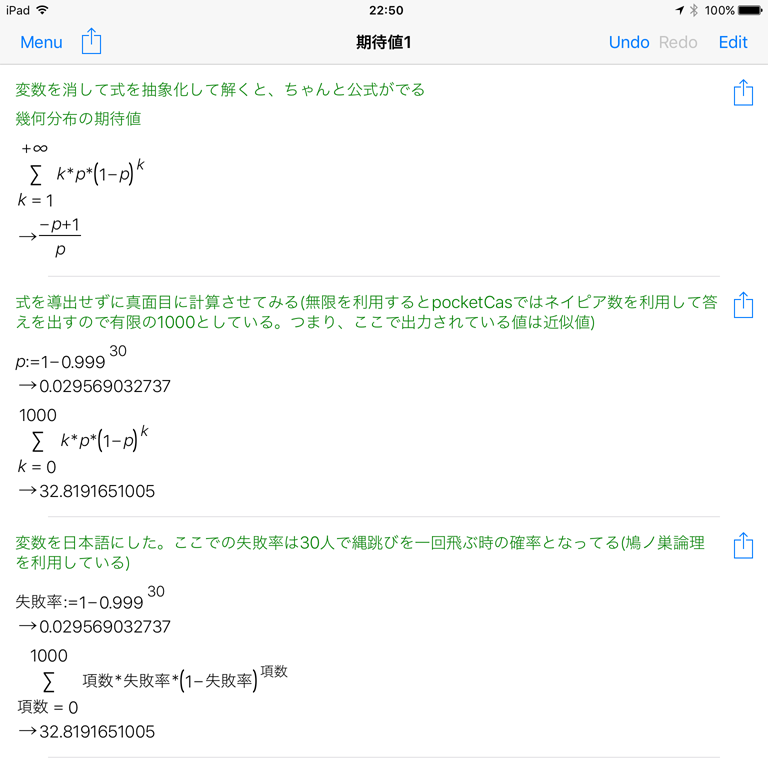
pocketCasで計算すると下記のように計算結果を出せるがこれを手作業で計算するのは大変すぎる

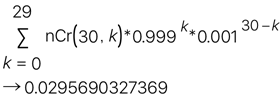
この失敗を計算する方法は実は確率の性質を利用する事で簡単に計算できる
確率の公理を利用すると以下のように考えられる（参考資料：数学ガール　乱択アルゴリズム　P124）

\(\Omega =\left\{ P=成功した事象,Q=失敗した事象 \right\} \\ 0\le Pr(P)\le 1\\ Pr(\Omega )=1\\ P\cap Q=\{ \} \quad \rightarrow \quad Pr(P\cup Q)=Pr(P)+Pr(Q)\)

ここで、\(成功確率p=Pr(P)\)。\(失敗確率q=Pr(Q)\)と考えると樹形図の成功以外の複数のルートをいちいち計算しなくても「\(q=(1-p)\)」である事がわかる
つまり、\(1-0.999^{ 30 }\)で「30人で縄跳びを一回跳ぶ事に失敗する確率」は求められる。このような考え方を資料：虚数の情緒ではP491～P492の鳩の巣原理で説明している

ここまでをまとめると...

• 30人で縄跳びを一回跳ぶ事に成功する確率は　\(p={0.999}^{30}\)
• 30人で縄跳びを一回跳ぶ事に失敗する確率は　\(q=1-{0.999}^{30}\)

ちなみに\(\{ { 0.999 }^{ 1 },{ 0.999 }^{ 2 },{ 0.999 }^{ 3 }\cdots { 0.999 }^{ 30 }\} \)と値が遷移していく様子をグラフで観察すると下図になる

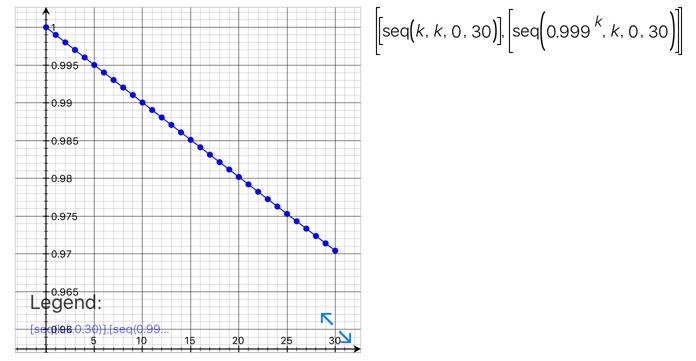
まるで一次関数グラフのように直線に見えるが0.999の部分の値を変えて観察すると下図になっている

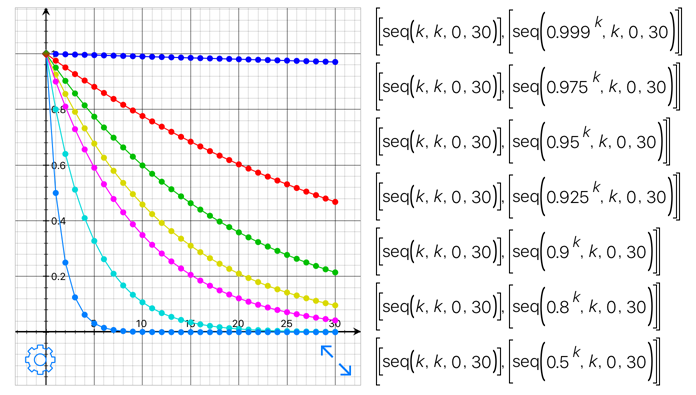
\({0.95}^{k}\)辺り（緑色の線グラフ）まで直線に近似しているがそれ以降に値が小さくなると曲線がより強くなっていく。一応知識として知っておくと後々何かに使えるかもしれないので併記しておく

＜おまけ＞
ちなみにpocketCasでは値を時間で変化させて視覚的にグラフの遷移をアニメーションで確認する事が出来ます。この画像の出力機能は対応されていないので実機で確認してください
非常に面白い動きをするので見ておくといいと思います

//!x=-9.25601..35.9059,y=-0.359563..1.20372,T=0.7..1,TStep=0.001
[seq(k,k,0,30)],[seq(T^k,k,0,30)]]

期待値を求める

＜TODO:以下工事中＞

確率は「起こり得る全体の中で希望するものの割合である」。この事を利用して希望するものの逆に該当する事象の確率を計算し全体である１から引き算することで答えを得る
この考えは数学的帰納と相性が良い。つまり、式がシグマやパイ（\(\sum { } \)や\(\prod { }\) ）等で表現できる。この積分計算は区分求積法となる。右端型、左端型でkの値は0もしくは1となる。

<期待値の定義より再確認>
\(\displaystyle \underbrace { E\left[ X \right] }_{ 期待値の入力Ｘは\\ ガウス記号に囲ま\\ れている } =\underbrace { \sum _{ \underbrace { k=1 }_{ 標本空間により0や1になる } }^{ \overbrace { \infty }^{ 標本空間の事象数であり極限を取るなら無限を使う } }{ \underbrace { { c }_{ k } }_{ 確率変数\\ がとる値。\\標本空間から1:1に対応した実数を返す関数 } } \cdot \underbrace { Pr\left( X={ c }_{ k } \right) }_{ 確率変数に対して\\ 確率（実数）を1：1で返す\\ 確率分布（関数）\\ } }_{ 「和集合」は「確率の和」になる。「確率変数×確率」の総和は「平均」となる } \)

確率（正規化された量：実数）を論じるとき、事象で構成された標本空間（集合）\(\Omega\)と、それに対応する確率分布（関数）\(Pr\)が必要となる
この問題に当てはまる、標本空間と確率分布を考えると・・・

• 確率変数\(X\)は「標本空間内の事象（集合）」に\(1:1\)で対応した実数を返すジェネリック関数
• 確率分布\(Pr\)は「確率変数である実数」に\(1:1\)で対応した確率（\(0\)以上\(1\)以下の実数）を返す関数

標本空間内の要素はこうなる
\(\Omega\)={\({\omega}_{1}\)=0回連続で飛んで1回目でひっかかった事象,
　　\({\omega}_{2}\)=1回連続で飛んで2回目でひっかかった事象,
　　\({\omega}_{3}\)=2回連続で飛んで3回目でひっかかった事象,
　　...,
　　\({\omega}_{n}\)=n-1回連続で飛んでn回目でひっかかった事象}

30人が縄跳びを連続で飛べた回数を確率変数\(X\)とする。つまり
\(X\left( \Omega \right) =\left\{ { c }_{ 1 }=0,{ c }_{ 2 }=1,{ c }_{ 3 }=2,\cdots { c }_{ n }=n-1 \right\} \quad \Leftrightarrow \quad X=\left\{ 0,1,2,\cdots n-1 \right\} \)

標本空間と確率変数との関係はシグマにより\(k\)がインクリメントされる事（\(k={ 1,2,3,\cdots ,n }\)の数列になる事）を利用して以下のように対応付けられる
\(X\left( \Omega \right) ={ c }_{ k }\left( { \omega }_{ k } \right) \)
この標本空間、確率変数に対応する確率分布（関数）は幾何分布となる（どんな関数が確率分布に合うか考えて適切な関数を用意する必要がある）

・・・なんかおかしい・・・？全部足し合わせて期待値になりそうにない気がする
あ、ちがう。３０人でけいさんしてない・・・あああ

鳩の巣原理2

資料：虚数の情緒P490
P493の確率リストをpocketCasで計算しグラフで表示してみる

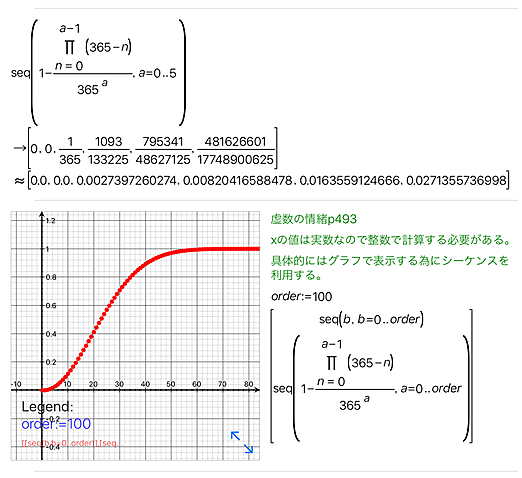
＜pocketCasでのコード＞

seq(1-(∏(365-n,n,0,a-1)/365^a),a=0..5)


order:=100
[[seq(b,b=0..order)],[seq(1-(∏(365-n,n,0,a-1)/365^a),a=0..order)]]

グラフはまるでフォトショップでのトーンカーブのようにＳ字で遷移している事が見て確認できる