ベクトル解析​/内積と正射影

内積

二つのベクトルの内積計算は\(\overrightarrow { A } \cdot \overrightarrow { B } \)と表され各ベクトルの各要素同士を掛け合わせ、その値を全て加算する事で行われる

\(\overrightarrow { A } =\left( \begin{matrix} x_{ A } \\ { y }_{ A } \\ z_{ A } \end{matrix} \right) \quad ,\quad \overrightarrow { B } =\left( \begin{matrix} x_{ B } \\ { y }_{ B } \\ z_{ B } \end{matrix} \right)\)
\(\overrightarrow { A } \cdot \overrightarrow { B } =x_{ A }\times x_{ B }+y_{ A }\times y_{ B }+z_{ A }\times z_{ B }\)

計算結果の値はベクトルにならずにスカラー（量:大きさ）になる事に注意。尚、ベクトルは太字でも表せるので以下のようにも書ける（今後はこの表記を利用する）
\(\mathbf { A } \cdot \mathbf { B } =x_{ A }\times x_{ B }+y_{ A }\times y_{ B }+z_{ A }\times z_{ B }\)

1 2 3 4

Vector3 a, b, dot; a = new Vector3 (1, 2, 3); b = new Vector3 (4, 5, 6); dot = Vector3.Dot (a, b); //unity標準の内積計算関数

このベクトルの内積は高校数学​/余弦定理と密接な関係がある。単刀直入に言うと内積 \(\mathbf { A } \cdot \mathbf { B }\) の計算結果は \(\left| \mathbf{A} \right| \left| \mathbf{B} \right| \cos { \theta } \) と同一になる
この事を利用してベクトルの正射影などが可能となる。これは後に証明を行う

\( \mathbf{A} \cdot \mathbf{B} =\left| \mathbf{A} \right| \left| \mathbf{B} \right| \cos { \theta } \)

この式の性質を利用する事により、ベクトル\(\mathbf { A }\)、\(\mathbf { B }\)の互いの方向の関係を内積計算することで知る事ができる

• \(\mathbf { A } \cdot \mathbf { B }\)が正の場合、∠ABつまりθは+-90°以内と判断できる
• \(\mathbf { A } \cdot \mathbf { B }\) が0の場合、ベクトルAとBは直交関係にある
• \(\mathbf { A } \cdot \mathbf { B }\)が負の場合、∠ABつまりθは+-90°以上と判断できる

これは式の右辺に \(\cos { \theta } \)がある事に起因する。ゲームコードでは視線を\(\mathbf { A }\)。主人公から見た敵の存在する方向ベクトルを\(\mathbf { B }\)とした時、この性質を利用する事により敵が視界前方にいるか。背後にいるかが判断できる

内積の証明

内積 \(\mathbf { A } \cdot \mathbf { B }\) の計算結果は \(\left| \mathbf{A} \right| \left| \mathbf{B} \right| \cos { \theta } \) と同一になる事の証明
(ベクトルとスカラーが式内で混じるので混乱しないようにする事。特に内積の計算中はベクトル扱いだが計算後はスカラーになっている点に留意)

三角形を構成する３つのベクトル\(\mathbf{abc}\)を描く

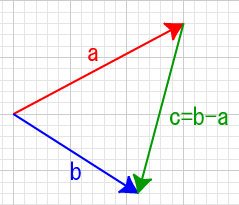
このベクトル\(\mathbf{c}\)は \(\mathbf{c=b-a}\)　により表せる

この\(\mathbf{c}\)を三平方の定理によりベクトルのスカラー（大きさ）を導く式は
\(\left| \mathbf{c} \right| =\sqrt { { (\mathbf{b-a}) }^{ 2 } }\)
\(\rightarrow \left| \mathbf{c} \right| =\sqrt { \mathbf{b\cdot b-2a\cdot b+a\cdot a} } \)
\( \rightarrow { \left| \mathbf{c} \right| }^{ 2 }=\mathbf{a\cdot a+b\cdot b-2a\cdot b}\)　　…①

となる。ここでベクトルの大きさの二乗は単ベクトルの内積計算になることを確認する

\(\left| \mathbf{ r } \right| =\sqrt { { x }_{ r }^{ 2 }+{ y }_{ r }^{ 2 }+{ z }_{ r }^{ 2 } } \\ \rightarrow { \left| \mathbf{r} \right| }^{ 2 }={ x }_{ r }^{ 2 }+{ y }_{ r }^{ 2 }+{ z }_{ r }^{ 2 }\\ \rightarrow { \left| \mathbf{r} \right| }^{ 2 }=\mathbf{r\cdot r}\)

①の単ベクトルの内積計算をベクトルの大きさに変換すると
\({ \left| { \mathbf{c} } \right| }^{ 2 }={ { \left| \mathbf{a} \right| }^{ 2 }+{ \left| { \mathbf{b} } \right| }^{ 2 }-2\mathbf{a\cdot b} }\quad \rightarrow \quad { c }^{ 2 }={ a }^{ 2 }+b^{ 2 }-2\mathbf{a\cdot b}\)　となる

どこがスカラーになっていて、どこからベクトルかしっかり認識する必要がある。赤字がスカラー。青地がベクトル
\(c^{ 2 }={ a }^{ 2 }+b^{ 2 }-2\)\(\mathbf{a\cdot b}\)

辺cの大きさを求める余弦定理の式を②として③を代入する
\(c^{ 2 }=a^{ 2 }+b^{ 2 }-2ab\cos { C }\)　…②
\(c^{ 2 }={ a }^{ 2 }+b^{ 2 }-2\mathbf{a\cdot b}\) …③

\(a^{ 2 }+b^{ 2 }-2ab\cos { C } ={ a }^{ 2 }+b^{ 2 }-2\mathbf{a\cdot b}\\ \rightarrow \quad \mathbf{a\cdot b}=ab\cos { C } \)

余弦定理の\(ab\)はスカラーなのでベクトルで考えると\(\left| a \right| \left| b \right| \)となる。よって

\(\mathbf{a\cdot b}=\left| \mathbf{a} \right| \left| \mathbf{b} \right|\cos { C } \)

上記のやりかた以外に下記のやり方もある

\(\mathbf{a}=\left( \begin{matrix} { x }_{ a } \\ y_{ a } \\ { z }_{ a } \end{matrix} \right) \quad ,\quad \mathbf{b}=\left( \begin{matrix} { x }_{ b } \\ y_{ b } \\ { z }_{ b } \end{matrix} \right) \quad ,\quad \mathbf{c=b-a}=\left( \begin{matrix} { x }_{ b }-{ x }_{ a } \\ y_{ b }-{ y }_{ a } \\ { z }_{ b }-{ z }_{ a } \end{matrix} \right) \\ \\ \left| \mathbf{c} \right| =\sqrt { { \left( { x }_{ b }-{ x }_{ a } \right) }^{ 2 }+{ \left( y_{ b }-{ y }_{ a } \right) }^{ 2 }+{ \left( { z }_{ b }-{ z }_{ a } \right) }^{ 2 } } \quad \rightarrow { \quad \left| \mathbf{c} \right| }^{ 2 }={ \left( { x }_{ b }-{ x }_{ a } \right) }^{ 2 }+{ \left( y_{ b }-{ y }_{ a } \right) }^{ 2 }+{ \left( { z }_{ b }-{ z }_{ a } \right) }^{ 2 }\\ \\ { \left| \mathbf{c} \right| }^{ 2 }={ \left( { x }_{ b }-{ x }_{ a } \right) }^{ 2 }+{ \left( y_{ b }-{ y }_{ a } \right) }^{ 2 }+{ \left( { z }_{ b }-{ z }_{ a } \right) }^{ 2 }\\ \quad \quad \quad ={ x }_{ b }^{ 2 }-2{ x }_{ a }{ x }_{ b }+{ x }_{ a }^{ 2 }+{ y }_{ b }^{ 2 }-2{ y }_{ a }y_{ b }+{ y }_{ a }^{ 2 }+{ z }_{ b }^{ 2 }-2z_{ a }z_{ b }+{ z }_{ a }^{ 2 }\\ \quad \quad \quad ={ x }_{ a }^{ 2 }+{ y }_{ a }^{ 2 }+{ z }_{ a }^{ 2 }\quad +\quad { x }_{ b }^{ 2 }+{ y }_{ b }^{ 2 }+{ z }_{ b }^{ 2 }\quad -2\left( { x }_{ a }{ x }_{ b }+{ y }_{ a }y_{ b }+z_{ a }z_{ b } \right) \\ \quad \quad \quad =\mathbf{a}\cdot \mathbf{a}+\mathbf{b}\cdot \mathbf{b}-2\mathbf{a}\cdot \mathbf{b}\\ \\ \mathbf{r}\cdot \mathbf{r}={ \left| \mathbf{r} \right| }^{ 2 }なので{ \left| \mathbf{a} \right| }^{ 2 }{ +\left| \mathbf{b} \right| }^{ 2 }-2\mathbf{a}\cdot \mathbf{b}\)

＜補足＞
\({ \mathbf{A} }\cdot { \mathbf{B} }=\left| { \mathbf{A} } \right| \left| { \mathbf{B} } \right| \cos { \theta } \quad\) の式を変形すると \(\displaystyle \quad \cos { \theta } =\frac { { \mathbf{A} }\cdot { \mathbf{B} } }{ \left| { \mathbf{A} } \right| \left| { \mathbf{B} } \right| } \quad \) となる。実際にcosθの値が求められるかunityで試してみる

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

- | | | - | | | | | | ! !

using UnityEngine; using System.Collections; public class VectorDot1 : MonoBehaviour { Vector3 vec1, vec2; float angle; void Start () { vec1 = new Vector3 (3, 0, 0); vec2 = new Vector3 (5, 0, 0); vec1 = Quaternion.AngleAxis (30, Vector3.forward) * vec1; angle = Vector3.Dot (vec1, vec2) / (vec1.magnitude * vec2.magnitude); print ("a・b/(|a||b|) = cosθ = " + angle); } }

出力:　a・b/(|a||b|) = cosθ = 0.8660254
コードではvec1をvec2に対して+30°傾けている。計算結果は0.8660254　となり、これはcos(30°)と一致する
つまり斜辺の長さ１。隣辺の長さcosθの計算が出来た事を意味する
証明どおりに内積の値の中にcosθが内包されている事が確認出来た

正射影

\(\mathbf{a}\)に\(\mathbf{b}\)を正射影したベクトル\(\mathbf{p}\)を求めたい

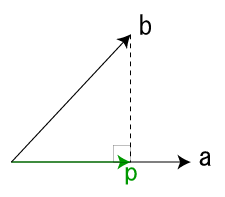
この場合の射影ベクトルを求める式は以下になる
\(\mathbf{ p }=\frac { \mathbf{a}\cdot \mathbf{b} }{ \mathbf{a}\cdot \mathbf{a} } \mathbf{a}\)

この正射影の計算はルート（平方根）の計算が混じっていないので非常に高速に動作する

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

- | | | - | | | | | | | ! !

using UnityEngine; using System.Collections; public class projection1 : MonoBehaviour { Vector3 a, b, proj, proj2; void Start () { a = new Vector3 (10, 4); b = new Vector3 (3, 7); proj = Vector3.Project (b, a); proj2 = (Vector3.Dot (a, b) / Vector3.Dot (a, a)) * a; print ("正射影unity標準機能＝" + proj + " 正射影自分で計算＝" + proj2); } }

正射影の証明

まず、正射影の式を作る

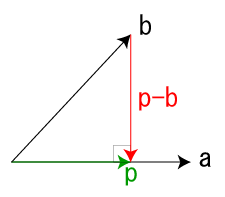
\(\mathbf{a}\)に\(\mathbf{b}\)を正射影したベクトル\(\mathbf{p}\)を求めたい。この際、\(\mathbf{b}\)から\(\mathbf{p}\)に向けてのベクトルは\(\mathbf{p-b}\)で表せる。
このベクトルは投影されるベクトル\(\mathbf{a}\)と直交関係にあるので

\(\left(\mathbf{ p-b} \right) \cdot \mathbf{a} =0\)　　・・・①

と表せる。（★：直交の関係を持つふたつのベクトル\(\mathbf{A}\)と\(\mathbf{B}\)は「\(\mathbf{A \cdot B}=0\)」という内積の方程式で表せる。これは非常に重要な計算テクニックとなっている）
また、ベクトル\(\mathbf{p}\)はベクトル\(\mathbf{a}\)と方向を同じとし未知数\(x\)スカラー倍された\(\mathbf{a}\)と言える。従って

\(\mathbf{p}=x\mathbf{a}\)　　・・・②

となる。この②を①に代入すると

\(\left( x\mathbf{a-b} \right) \cdot \mathbf{a}=0\) となり、これを展開すると \(x\mathbf{a}\cdot \mathbf{a-a}\cdot \mathbf{b}=0\quad \rightarrow \quad x\mathbf{a}\cdot \mathbf{a}=\mathbf{a}\cdot \mathbf{b}\quad \rightarrow \quad x=\frac { \mathbf{a}\cdot \mathbf{b} }{ \mathbf{a}\cdot \mathbf{a} }\) となる。\(x\)の式が判明したのでこれを②に代入すると

\(\mathbf{p}=\frac { \mathbf{a}\cdot \mathbf{b} }{ \mathbf{a}\cdot \mathbf{a} } \mathbf{a}\) という正射影の式が完成する

この式が何故正射影になるのかを調べてみる

\(\mathbf{p}=\frac { \mathbf{a}\cdot \mathbf{b} }{ \mathbf{a}\cdot \mathbf{a} } \mathbf{a}\)

まず、内積は\(\mathbf{a\cdot b}=\left| \mathbf{a} \right| \left| \mathbf{b} \right|\cos { C }\)だった。又、\({ \left| \mathbf{a} \right| }^{ 2 }=\mathbf{a\cdot a}\)であるので式は以下のように変形される

\(\displaystyle\mathbf{p}=\frac { \left| \mathbf{a} \right| \left| \mathbf{b} \right| \cos { \theta } }{ { \left| \mathbf{a} \right| }^{ 2 } } \mathbf{a}\) この式を整理していくと...

\(\displaystyle\rightarrow \quad \mathbf{p}=\left| \mathbf{a} \right| \left| \mathbf{b} \right| \cos { \theta } \frac { \mathbf{a} }{ { \left| \mathbf{a} \right| }^{ 2 } } \)

\(\displaystyle\rightarrow \quad \mathbf{p}=\left| \mathbf{a} \right| \left| \mathbf{b} \right| \cos { \theta } \frac { \mathbf{a} }{ \left| \mathbf{a} \right| \left| \mathbf{a} \right| } \)

\(\displaystyle\rightarrow \quad \mathbf{p}=\left| \mathbf{b} \right| \cos { \theta } \frac { \mathbf{a} }{ \left| \mathbf{a} \right| }\)

\(\displaystyle\frac { \mathbf{a} }{ \left| \mathbf{a} \right| } \)はベクトル\(\mathbf{a}\)の単位ベクトル\({ \mathbf{e} }_{ a }\)となる

\(\displaystyle\rightarrow \quad \mathbf{p}=\left| \mathbf{b} \right| \cos { \theta } \times { \mathbf{e} }_{ a }\)

この最後の状態まで変形させると式の意味がわかりやすくなる。つまり\(\left| \mathbf{b} \right|\)スカラー倍された\(\cos { \theta }\)が単位ベクトル\( {\mathbf{e} }_{ a }\)に掛算されている。これが正射影の正体となっている

• Prev
• ベクトル解析