単位計算 [微積分と物理/単位計算]

[ トップ ] [ 差分 | バックアップ | リロード ] [ 新規 | 一覧 | 検索 | 最新 | ヘルプ ]

メニューバー

抽斗

単位計算

何故、単位計算のような事を今考え直すかというと「速度の逆数」や「速度同士の比」の有効利用を理解する為。これらには具体的にその概念を指す名前が無い
つまり日常に行う計算の中で、これらを利用した計算は"非常に直観的に解り難い"
この場合、計算を単位で考えるとシンプルに計算結果とその過程である道筋の意味が掴める

速度とは分母、分子を持つ有理数か無理数、そして傾きになる。分子分母の単位は小学校で習う、距離(km)＝速度(km/h)×時間(h)のようなモノがある
この場合、速度の分母は時間(h)であり分子は距離(km)、これを一般常識として「時間を１単位とした速度」と扱っている

では、この分母分子の逆をどう考えるか？速度の逆数。つまり距離の方が「１単位」になる。どうやら掛算や割算は単位変換となりうると考えられる
計算では「1÷分数」をするとその答えは、そのひっくり返った分数、「逆数」になる
しかし、繁分数の様に分母に有理数の足算がされたらどうなるだろうか？　この計算はどういった意味になって行くのだろうか？

\(\displaystyle \sqrt { 2 } =1+\frac { 1 }{ 2+\frac { 1 }{ 2+\frac { 1 }{ 2+\frac { 1 }{ 2+\frac { 1 }{ 2 } \\ \vdots } } } } \)

この式は分解していくと、等差数列で表せるのか？等比数列？階差数列？

＜これから確かめる＞
繁分数は漸化式で表せるか？
繁分数は一般式で書き表せるのか？
繁分数はシグマで書き表せるのか？

不思議な計算

指数法則で\(-1\)乗すると逆数になる

\({ 2 }^{ -1 }=\frac { 1 }{ 2 } \)

\({ 2 }^{ -2 }=\frac { 1 }{ 4 } \)

\({ \left( \frac { 1 }{ 2 } \right) }^{ -1 }=2\)

\({ \left( \frac { 1 }{ 2 } \right) }^{ -2 }=4\)

\(\frac { 2 }{ \sqrt { 2 } } =\sqrt { 2 }\)

\(\frac { 1 }{ \sqrt { 2 } } \simeq 0.7071...\)

\(\frac { \sqrt { 2 } }{ 2 } ={ \sqrt { 2 } }^{ -1 }=0.7071...\)

\(0.7071...\times \sqrt { 2 } \simeq 1\)

\(0.7071...\times 2\simeq \sqrt { 2 } \)

\(\frac { 2 }{ 0.7071...\times 2 } =\frac { 1 }{ 0.7071... } \simeq \sqrt { 2 } \)

\(\sin { (45°)=0.7071... }\)

\(\cos { (45°)=0.7071... } \)

ネイピア数

\(\displaystyle e=\lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ n } \right) }^{ n } } \simeq 2.71828....\)

アキレスと亀

資料：ゼノンのパラドックス

あるところにアキレスと亀がいて2人は徒競走をすることとなった。アキレスの速度が\(a(km/h)\)。亀の速度が\(b(km/h)\)。\(a>b\)であり、アキレスの方が足が速いのは明らかなので亀がハンディキャップをもらって、\(c (km)\)先に進んだ地点からスタートする事となった

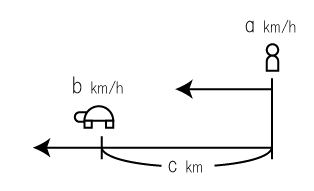
①競争開始、アキレスが亀がいた位置まで移動する時間

\(\displaystyle c\quad (km)\quad \times \quad \frac { 1 }{ a } \quad \left( \frac { h }{ km } \right) \quad =\quad \frac { c }{ a } \quad (h)\)

有限個の和を前提とした計算の為、有理数の体を守るように計算を加算、乗算で統一する（減算、除算は利用しない。その方が計算の運用がやり易い）。アキレスの速度は実数の切断定義より有理数の集合である事が解っているので分数の比を逆にして除算を表現し逆数とした。速度を逆数にした事で単位も分子分母がひっくり返っている

②その間に亀が動く距離

\(\displaystyle \frac { c }{ a } \quad (h)\quad \times \quad b\quad \left( \frac { km }{ h } \right) \quad =\quad \frac { c }{ a } \cdot b\quad (km)\)

③亀の移動先にアキレスが追い付く時間

\(\displaystyle \frac { c }{ a } \cdot b\quad (km)\quad \times \quad \frac { 1 }{ a } \quad \left( \frac { h }{ km } \right) \quad =\quad \frac { c }{ a } \cdot \frac { b }{ a } \quad (h)\)

④その間に亀が動く距離

\(\displaystyle \frac { c }{ a } \cdot \frac { b }{ a } \quad (h)\quad \times \quad b\quad \left( \frac { km }{ h } \right) \quad =\quad \frac { c }{ a } \cdot \frac { b }{ a } \cdot b\quad (km)\)

⑤アキレスが④に追い付く時間

\(\displaystyle \frac { c }{ a } \cdot \frac { b }{ a } \cdot b\quad (km)\quad \quad \times \quad \frac { 1 }{ a } \quad \left( \frac { h }{ km } \right) \quad =\quad \frac { c }{ a } \cdot \frac { b }{ a } \cdot \frac { b }{ a } \quad (h)\)

以後、②～③、④～⑤、の様に同じ計算を繰り返す事となる。この計算を無限回数だけ試行する事を考えると
アキレスは亀に追いついても亀はさらにその先にいることになり結果、永遠にアキレスは亀に追いつけない事になる

しかし、ここで無限個の和、無限級数の計算を適用すると、このパラドックスは解消される
つまり等比数列の総和=シグマで考える。アキレスが亀に追いつく時間の計算は

\(\displaystyle \frac { c }{ a } +\left( \frac { c }{ a } \cdot \frac { b }{ a } \right) +\left( \frac { c }{ a } \cdot \frac { b }{ a } \cdot \frac { b }{ a } \right) +\cdots \quad \quad (h)\)

のような計算となる。この「アキレスが亀に追いつく時間」はシグマで表すと

\(\displaystyle \frac { c }{ a } \sum _{ k=1 }^{ \infty }{ { \left( \frac { b }{ a } \right) }^{ k-1 } } \quad \quad (h)\)

になる。アキレスは亀よりも走るのが早い。つまり\(a>b\)。従って\(\frac { b }{ a } \)は１未満になる
これは等比数列の総和で考えた時、無限級数の計算の条件

\(\displaystyle \lim _{ n\rightarrow \infty }{ { S }_{ n }= } \lim _{ n\rightarrow \infty }{ \sum _{ k=1 }^{ n }{ { a }_{ 1 }{ r }^{ k-1 } } } =\sum _{ k=1 }^{ \infty }{ { a }_{ 1 }{ r }^{ k-1 } } =\frac { { a }_{ 1 }\left( 1-0 \right) }{ 1-{ r } } =\frac { { a }_{ 1 } }{ 1-{ r } } \quad \quad (-1<r<1)\)

を満たしている。これにより分子の指数が肩にある等比変数\(r\)に収束が発生する。実際に計算してみる。等比数列の公式より\({ a }_{ n }={ a }_{ 1 }{ r }^{ n-1 }\)に当てはめると

\({ a }_{ 1 }=\frac { c }{ a } \quad (h)\quad ,\quad r=\frac { b }{ a } \quad \left( \frac { \frac { km }{ h } }{ \frac { km }{ h } } =単位がなくなる。従って純粋な比。傾きとなる \right) \)　なので

これを無限級数の式に当てはめる。分数の1の変形を利用して式を変形すると「アキレスが亀に追いつく時間」は

\(\frac { c }{ a } \cdot \frac { 1 }{ 1-\frac { b }{ a } } \quad =\quad \frac { c }{ a } \cdot \frac { 1\cdot a }{ \left( 1-\frac { b }{ a } \right) \cdot a } \quad =\quad \frac { c }{ a } \cdot \frac { a }{ a-b } \quad =\quad \frac { c }{ a-b } \quad (h)\)

となる。この計算で起きたことを少しまとめておきます

等比数列の公比\(r\)に\(1\)未満の値が生じると級数計算に変わり等比に対しての\(0\)への収束が発生した
アキレスが亀に追いつけないパラドックスはこれにより解消されている
無限級数の公比\(r\)に単位の消滅があった。速度同士の割算は単位が消滅して純粋な比になる事がある
理屈で考えると単位が消滅した比の値に対して乗算除算で単位が付加される。除算の場合は(1/単位：単位比)みたいな事も可能となる
結局、人類は今のところ\(0\)を無限小として見てるって事らしい

方程式との合致

これは中学までの計算（旅人算）で、かかる時間を\(t\)として方程式にすると

\(\begin{cases} bt+c\quad \cdots 亀の進んだ距離 \\ at+0\quad \cdots アキレスの進んだ距離 \end{cases}\)

この連立方程式を\(t\)について解くと「アキレスが亀に追いつく時間」は

\(at=bt+c\quad \rightarrow \quad at-bt=c\quad \rightarrow \quad t(a-b)=c\quad \rightarrow \quad t=\frac { c }{ a-b } \)

となり、計算結果が無限級数の計算結果と合致する

アルキメデスの公理

ふたつの数、\(\varepsilon,a\)を考える。ここで\(\varepsilon\)が如何に小さい数で\(a\)が如何に大きな数\(\left( \varepsilon <a \right) \)であったとしても、\(n\varepsilon>a\)となる自然数\(n\)が必ず存在する。これをアルキメデスの原則と言う。これは\(n\)が自然数である点が非常に重要で、つまり

\(n\varepsilon>a\) は

\(\displaystyle \underbrace { \varepsilon +\varepsilon +\varepsilon +\varepsilon +\cdots +\varepsilon }_{ \times n } >a\)を意味し

無限大のn個の\(\varepsilon\)の総和は必ずaより大きくなる事を意味している
（ここで自然数が使われる事によって実数の定義に狂いなく定義通りの切断が行える）

大小を逆にして\(n\varepsilon <a\quad \rightarrow \quad \varepsilon <\frac { a }{ n } \)とした場合、\(\frac { a }{ n } \)はガンガン小さくなるので\(\varepsilon=0\)(無限小）にならざる得なくなる

これが\(\displaystyle \lim _{ n\rightarrow \infty }{ \frac { 1 }{ n } } =0\)の基礎になっている

資料：「虚数の情緒」P450

無限小と無限大

資料：無限小(wikipedia)

如何に小さい数＝無限小
如何に大きい数＝無限大

とすると間違う。無限小は欲すれば欲するだけ小さくなる、無限大は欲すれば欲するだけ大きく変動する常に更新され続ける変数のようなものだから
比べる瞬間にそれは更新され大小を比べる意味は無くなる筈。つまり無限小、無限大は数ではなく仮想的な概念だから
必ず「限りなく近くなる（lim）」という言葉を加えて「すぐ隣の定数に点を作成」して数直線上に固定させ大小を比べられる様にしなければならない