微積分と物理​/実数の定義

数は数直線状の切断によって「表現される」。この切断をデデキント切断と言う

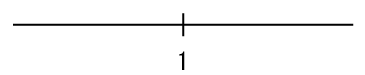
数直線上の\(1\)を基準にふたつの有理数の集合に切断してみる。片方を\(A\)、もう片方を\(B\)とする
このふたつの集合を組みにした\((A,B)\)を「切断」と呼び、切断そのものを理論上の「実数」とみなすことにする
(\(A\)と\(B\)は同じ値として扱われる。好みで、どちらの表現をしても良い)
切断は以下の論理命題で定義される

1. \(\mathbb{Q}=A\cup B\)
2. \(A\cap B=\emptyset ,A≠\emptyset ,B≠\emptyset \)
3. \(a\in A,b\in B\quad \Rightarrow \quad a\le b\)
4. \(A\in \mathbb{Q}\quad ,\quad A≠\mathbb{Q} \)
5. \(A\)には最大値が無い
6. \((a\in A\quad \wedge \quad t\in \mathbb{Q} \quad \wedge \quad t<a)\quad \Rightarrow \quad t\in A\)

\(A\)と\(B\)を合わせた集合は有理数の集合となる。これらは空集合を含まない
\(a\)が\(A\)の集合に属し、\(b\)が\(B\)の集合に属すならば、\(a\le b\)が成り立つ
\(A\)は有理数で、有理数の全体と同じではない。つまり有理数\(\mathbb{Q}\)の部分集合
\(A\)は最大値を持たないが認識できる有理数\(t\)よりも大きな値\(a\)を見つける事により無限に大きくなり続ける。従って集合\(A\)は上界を持つ

切断の境目は無理数である場合と、有理数の場合である時の2種類がある

有理数の場合は、その境目をどちらかの集合に入れて置く事になるので、ここでは集合\(B\)に入れる事に決めた

上記の条件を踏まえて実際に\(1\)を基準に切断すると、その切断の境目は有理数の\(\frac { 3 }{ 3 } \)となる為以下になる
\(切断\left( \quad A:=\left\{ a\in { \mathbb{Q} }|a<1 \right\} \quad ,\quad B:=\left\{ b\in { \mathbb{Q} }|b\ge 1 \right\} \quad \right) \quad \Rightarrow \quad 切断\left( \quad \frac { 1 }{ 3 } \times 3=0.\dot { 3 } \times 3=0.\dot { 9 } \quad ,\quad \frac { 3 }{ 3 } =1\quad \right) \)
\(\Rightarrow \quad 切断\left( \quad 0.\dot { 9 } \quad ,\quad 1 \quad \right) \)

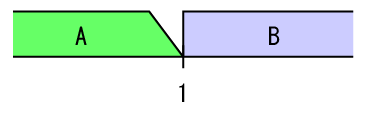
\(a\)は有理数なので以下のようにも表せる。このように考えると実数と有理数、極限の関係が掴めてくる
\(\displaystyle a\quad =\quad \lim _{ n\rightarrow \infty }{ 1-\frac { 1 }{ { 10 }^{ n } } } \quad =\quad 0.\dot { 9 } \)

補足：
\(a= \lim _{ n\rightarrow \infty }{ 1-{ \left( \frac { 1 }{ { 10 } } \right) }^{ n } } \)も同様になる
\(a= \lim _{ n\rightarrow \infty }{ { \left( 1-\frac { 1 }{ { 10 } } \right) }^{ n } } \)等とすると式の意味が全く変わってくるので注意（この場合は二項定理が必要になってきて計算結果も大きく変わる）

このように切断により集合\(B\)に必ず最小値の端を持つ事になり集合\(A\)と重なって数としての穴は開かないようになる。つまり「実数の連続性」はこれによって得られる
ここで、この理屈が正しいことを計算機を使って確認してみる（実際に計算機を用意して以下を試す）

\(1\div 9=0.11111...=0.\dot { 1 } \\ 2\div 9=0.22222...=0.\dot { 2 } \\ 3\div 9=0.33333...=0.\dot { 3 } \\ \quad \quad \quad \vdots \\ 8\div 9=0.88888...=0.\dot { 8 } \\ 9\div 9=0.99999...=0.\dot { 9 } =1\)

有理数の境目を使って\(切断（A,B）\)を利用すると「切断（ 連続として重なっている隣の点の実数表現 , ジャストの有理数表現 ）」が得られる。\(A\)も\(B\)も有限の紙の上で書ける表現となる。反対に紙に書けない無理数のような無限に続く実数の値は一端、有理数の近似値にして近似の実数を得るしかない

上記の証明の逆パターン。この証明でも切断の境目はどちらかの集合に含まれている

どんな実数\(r\)に対しても、\(r\)より大きい有理数\(a\)と、\(r\)より小さい有理数\(b\)がある

\(r\in \mathbb{Q}\quad ,\quad r≠\mathbb{Q}\quad ,\quad r≠\emptyset \)

\(r\)は有理数の部分で空集合でない

\(r\left( a,b \right) =\left( \left\{ a\in \mathbb{Q}\wedge a\notin r｜a>r \right\} ,\left\{ b\in \mathbb{Q}\wedge b\in r｜b\le r \right\} \right) \)

\(r\)は有理数の部分集合なので\(a\notin r\)であるような有理数を勝手に取る。\(a\)を実数としてみると\(a>r\)となる。\(b\)は\(b\in r\)となるような値を取る。実数の定義を切断を使うと、このように証明できる

無理数の場合

\(r\)が無理数と考えた場合、こうなる？（あってるかわからない）
切断の境目がどちらの集合の中にも含まれていない。有理数の切断が二つの組に最大値も最小値も作りえない時、その"切断"が無理数を定義する

\(r\left( a,b \right) =\left( \left\{ a\in \mathbb{Q}\wedge a\notin r｜a<r \right\} ,\left\{ b\in \mathbb{Q}\wedge b\notin r｜b>r \right\} \right) \)

自然数から整数、整数の比から有理数になり、有理数の切断から無理数が生まれ実数となる
無理数が切断の境目に使用された場合、数の隙間が発生する。この隙間を埋め続けるような「永遠に割り切れない循環しない数＝無理数」となる

---

資料：「虚数の情緒」P454はこのデデキント切断を指して説明している