微分 [微積分と物理/微分] - Unity学習帳２冊目

＜注意：このページの書いてある事はかなり好き勝手にやってます＞
適当に思考実験で以下で色々式をこねまわしていますが、こんなやりかたで漸化式を作っている例がみつかりません・・・
色々調べているのですが、たぶん、無茶苦茶なやりかたなのだと思います。ただ漸化式は作れているので、数式の書き方が数学の文法にのっとってないのだと思います
常識的に変な書き方をしてしまっていると思いますので、今後調べて正しい書き方に直す予定です。ここに書いてある事を真面目に受け取らないようにお願いします

＜メモ（考察中）＞

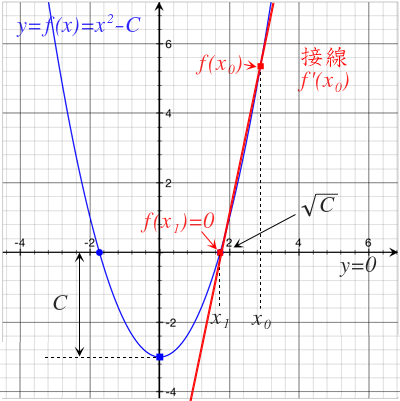
微分を利用して平方根を求める

微分の基礎的な式

\(\displaystyle\ f'(a)=\lim _{ b→a }{ \frac { f(b)-f(a) }{ b-a } } \)

\( f'(a) \)はグラフの接線の傾きを示す

この式に上グラフ図の関係を当てはめて考えると以下の連立方程式を作る事が出来る

\(\displaystyle\ \begin{cases} f'({ x }_{ 1 })=\lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ \frac { f({ x }_{ 0 })-f({ x }_{ 1 }) }{ { x }_{ 0 }-{ x }_{ 1 } } } \quad \cdots ① \\ y=f({ x }_{ 1 })=0\quad \quad \quad \quad \quad \cdots f({ x }_{ 1 })における関数の出力の値を0に固定している。これにより①の右辺分母の{ x }_{ 1 }の値が決定する\quad \\ y=f(x)={ x }^{ 2 }-C \end{cases}\)

この連立方程式を\({x}_{1}\)に対して解くと\({ x }_{ 1 }\ge \pm \sqrt { C } \)となる。以下で実際に解いてみる。仮に\(C\)を\(3\)として、\(f'({x}_{1})\)を形式的微分で導関数にして①にあてはめると
（要：今後の考察 \(f'({x}_{1})=2{x}_{0}\)になる理由は良く考えた方が良さそう？？？自分自身よくわかってない。基礎的な式に沿うならば\(2{x}_{1}\)のような…）

\(\displaystyle\ 2{ x }_{ 0 }=\lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ \frac { { x }_{ 0 }^{ 2 }-3-0 }{ { x }_{ 0 }-{ x }_{ 1 } } } \)
\(\rightarrow \displaystyle\ \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ 2{ x }_{ 0 }({ x }_{ 0 }-{ x }_{ 1 })={ x }_{ 0 }^{ 2 }-3 } \)　(この時、左辺まで極限の範囲を伸ばしているがこれは「して良い事」なのだろうか？？？)
\( \rightarrow \displaystyle\ \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ 2{ x }_{ 0 }^{ 2 }-{ 2x }_{ 0 }{ x }_{ 1 }={ x }_{ 0 }^{ 2 }-3 } \)
\( \rightarrow \displaystyle\ \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ -{ 2x }_{ 0 }{ x }_{ 1 }={ -x }_{ 0 }^{ 2 }-3 } \)
\( \rightarrow \displaystyle\ \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { 2x }_{ 0 }{ x }_{ 1 }={ x }_{ 0 }^{ 2 }+3 } \) … ②

少し考えてみたのだが極限適用前と適用後では導関数の入力が変わるのではと考えてみた
極限適用前は傾きである\(f'(x)\)は\(f'({x}_{0})\)であり適用後は\({x}_{0}\)→\({x}_{1}\)と近づくので\(f'({x}_{1})\)と変化する
書籍などで基礎的な式として紹介されている微分の式の左辺\(f'(a)\)は極限計算後の傾きを示していると考えられる？？？

ここからふたつの式の展開方法がある
まず極限を利用して収束する値を②から求めてみるパターン
\(\displaystyle\lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { 2x }_{ 0 }{ x }_{ 1 }={ x }_{ 0 }^{ 2 }+3 } \)
\(\displaystyle\rightarrow \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { x }_{ 0 }^{ 2 }-{ 2x }_{ 0 }{ x }_{ 1 }+3=0 }\) 片方の辺に集めて極限を適用すると
\(\rightarrow { x }_{ 1 }^{ 2 }-{ 2x }_{ 1 }{ x }_{ 1 }+3=0\)
\(\rightarrow { x }_{ 1 }^{ 2 }-2{ x }_{ 1 }^{ 2 }+3=0\)
\(\rightarrow -{ x }_{ 1 }^{ 2 }+3=0\)
\(\rightarrow -{ x }_{ 1 }^{ 2 }=-3\)
\(\rightarrow { x }_{ 1 }^{ 2 }=3\)
\(\rightarrow { x }_{ 1 }=\pm \sqrt { 3 } \)

つまり極限を取って\({x}_{0}\)から\({x}_{1}\)へとぎゅ～っと近づけると\({x}_{1}\)は\(\sqrt { C } \)へと収束する。微分を理解するとこういう事が出来る
接線の傾きが得られる微分の形式的微分である導関数を利用して\(y=f({x}_{1})=0\)の時との連立方程式を組み「\({x}_{1}\)」を逆算してルートの値を求めている

極限から収束する値は分ったので今度はその具体的な実数値を計算する式を得てみる。②から\({x}_{1}\)に対する漸化式を作る

\(\displaystyle\ \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { 2x }_{ 0 }{ x }_{ 1 }={ x }_{ 0 }^{ 2 }+3 } \)
\(\displaystyle\ \rightarrow \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { x }_{ 1 }=\frac { { x }_{ 0 }^{ 2 }+3 }{ { 2x }_{ 0 } } } \)
\(\displaystyle\ \rightarrow \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { x }_{ 1 }=\frac { 1 }{ 2 } \left( \frac { { x }_{ 0 }^{ 2 }+3 }{ { x }_{ 0 } } \right) } \)
\(\displaystyle\ \rightarrow \lim _{ { x }_{ 0 }→{ x }_{ 1 } }{ { x }_{ 1 }=\frac { 1 }{ 2 } \left( { x }_{ 0 }+\frac { 3 }{ { x }_{ 0 } } \right) } \)

ここで極限のついた「平方根を求めるバビロニア式アルゴリズム」「ニュートン法」に似た式が出てきた
極限は\({x}_{0}→{x}_{1}\)となっていて、これを漸化式にすると

\(\displaystyle\ x_{ n+1 }=\frac { 1 }{ 2 } \left( { x }_{ n }+\frac { 3 }{ { x }_{ n } } \right) \)

になる。この漸化式の\({x}_{n}\)に適当な値を入れて２～６回計算を繰り返すと\( \sqrt { 3 } \)の近似値が得られる
この漸化式の右辺は高校数学/相加相乗平均の関係 \(\frac { a+b }{ 2 } \ge \sqrt { ab }\) の左辺と非常によく似ている

ここで相加相乗平均の関係式を\(a={ x }_{ n },b=\frac { 3 }{ { x }_{ n } } \)と考えて相加相乗平均を求めると\( x_{ n+1 }=\frac { \left( { x }_{ n }+\frac { 3 }{ { x }_{ n } } \right) }{ 2 } \ge \sqrt { { x }_{ n }\cdot \frac { 3 }{ { x }_{ n } } } =\sqrt { 3 } \)となる
（このような式の組み方はあまり見慣れないが、いろいろな情報を一度に提示している）
この式により漸化式の答えが恒久的に\(\sqrt{3}\)以上になる事が確認できる。計算を繰り返すたびに必ず答えは\(\sqrt{3}\)以上になり\(\sqrt{3}\)に近似していく

どうやら極限と漸化式には密接な関係があるように思える。今後、漸化式と極限の関係を調べて行こうと思う

memo..
微積分は根底に数列に対する何らかの操作が含まれている。漸化式もその計算の度に出てくる値の数列なのかもしれない