|
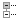
<注意:このページの書いてある事はかなり好き勝手にやってます> memo:常微分方程式 4乗根の実数値を求める漸化式を作る
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| - | - | | | | | - | | ! | ! ! | |
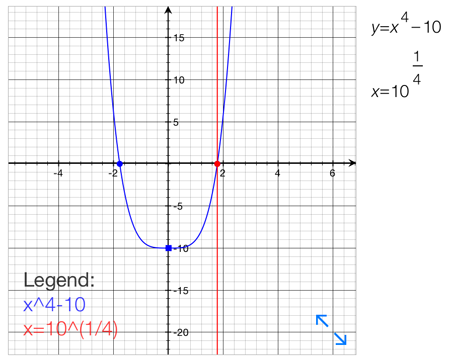
結果出力された値は 1.778279 となり、これは\(\sqrt [ 4 ]{ 10 } \simeq 1.778279\)を表しているので漸化式が正常に機能している事がわかる
\(1.778279\times 1.778279\times 1.778279\times 1.778279\simeq 10\)
memo:
ある特定の横x縦yのグラフがあったとして、ある関数が描くグラフのyの位置時のxの値を知りたい時に
導関数と微分の式で連立方程式を組んで逆算できる。つまりyになるであろうxを導関数から逆算して計算できる
本来、計算機で計算するなら元の関数(元の関数は導関数を積分したものだから)から逆算した方が早い
物理的に考えるなら位置の関数があって、位置の値から時間を求めたいなら位置の関数を利用する方が手っ取り早い
もし手元に速度の関数しかないなら、それを積分して位置の関数にして逆算する
微積分のメリットは例えるなら「速度の情報しかない時に位置を想定して時間を計算できる」という部分にある
そこに、このような漸化式は「有限回の直接計算をして無限、極限回計算の近似を計算する」という機能を加える
漸化式の計算は複数回繰り返す必要があるので重い処理となる
累乗根や対数など計算機に任せられる部分があるなら積分して位置の関数から値を計算する方が良い
・・もう少し具体的な例を考えてみる
物理的な値を求める漸化式を作ってみる 
思考実験として物理的な値を求める漸化式を作る
<問題>
速度\(v=9.8t\) で移動する物体がある。この物体が700m先の位置を通過する時間を知りたい
この問題を解くため微分積分にあてはめると \(v=9.8t\) を形式的積分の式である \(a{ x }^{ n }\quad \mapsto \quad a\frac { 1 }{ n+1 } { x }^{ n+1 }\) に通すと
\(v=9.8{ t }^{ 1 }\quad \mapsto \quad y=9.8\frac { 1 }{ 1+1 } { t }^{ 1+1 }\quad \rightarrow \quad y=4.9{ t }^{ 2 }\) となる
\(y=4.9{t}^{2}\) は距離の関数なので\(y=700\)との連立方程式を解けばよい
\(\begin{cases} y=4.9{ t }^{ 2 } \\ y=700 \end{cases}\quad \rightarrow \quad 4.9{ t }^{ 2 }=700\quad \rightarrow \quad { t }=\sqrt { \frac { 700 }{ 4.9 } } =11.952...\)・・・①
11.952秒後に通り過ぎる。この計算をする時、電卓に\(\sqrt { }\)キーや\(\log { } \)キーがない。対数表も持ってない
「微積分が無限、極限回数の計算を繰り返してたどり着く答えを得ている事を実感できない」時は以下のようにする
\(f'(a)=\lim _{ b\rightarrow a }{ \frac { f(b)-f(a) }{ b-a } } \quad \mapsto \quad 9.8{ t }_{ 0 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ \frac { 4.9{ t }_{ 0 }^{ 2 }-700 }{ { t }_{ 0 }-{ t }_{ 1 } } } \)
\(9.8{ t }_{ 0 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ \frac { 4.9{ t }_{ 0 }^{ 2 }-700 }{ { t }_{ 0 }-{ t }_{ 1 } } } \quad \rightarrow \quad 9.8{ t }_{ 0 }\left( { t }_{ 0 }-{ t }_{ 1 } \right) =\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ 4.9{ t }_{ 0 }^{ 2 }-700 } \quad \rightarrow \quad 9.8{ t }_{ 0 }^{ 2 }-9.8{ t }_{ 0 }\cdot { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ 4.9{ t }_{ 0 }^{ 2 }-700 } \\ \)
\(\rightarrow \quad -9.8{ t }_{ 0 }\cdot { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ -4.9{ t }_{ 0 }^{ 2 }-700 } \quad \rightarrow \quad 9.8{ t }_{ 0 }\cdot { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ 4.9{ t }_{ 0 }^{ 2 }+700 } \quad \rightarrow \quad { t }_{ 0 }\cdot { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ \frac { 4.9 }{ 9.8 } { t }_{ 0 }^{ 2 }+\frac { 700 }{ 9.8 } } \\ \)
\(\rightarrow \quad { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ \frac { 4.9 }{ 9.8 } { t }_{ 0 }+\frac { 700 }{ 9.8{ t }_{ 0 } } } \quad \rightarrow \quad { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ \frac { 1 }{ 2 } { t }_{ 0 }+\frac { 700 }{ 9.8{ t }_{ 0 } } } \quad \rightarrow \quad { t }_{ 1 }=\lim _{ { t }_{ 0 } \rightarrow { t }_{ 1 } }{ \frac { 1 }{ 2 } \left( { t }_{ 0 }+\frac { 700 }{ 4.9{ t }_{ 0 } } \right) } \\ \)
\(\rightarrow \quad { t }_{ n+1 }=\frac { 1 }{ 2 } \left( { t }_{ n }+\frac { 700 }{ 4.9{ t }_{ n } } \right) \\ \)・・・②
この最期の漸化式をコードにすると以下になる
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| - | - | | | | | - | | ! | ! ! | |
t0の値はどんな値を入れても良い。このコードでは5000回計算を繰り返しているが、微分も積分も無限回数この計算を繰り返している事になる。その答えは必ず、\(11.952...\)へと収束する。微分積分はこの仕組みを利用してコンパクトに値を求めているらしい
![[PukiWiki] [PukiWiki]](http://unitylabo.s601.xrea.com/xoops/modules/xpwiki/image/pukiwiki.png)