関数の極限 
関数の式を扱う際、ある存在しない値を計算する際に極限が必要になる事があります
一例をあげると下記のような場合です
\(\displaystyle f(x)=\frac { { x }^{ 2 }-6x+8 }{ x-2 } \)
この関数は\(x\)が\(2\)の時、分母に\(0\)の除算が発生し計算不能となります
\(\displaystyle f(2)=\frac { 2^{ 2 }-6\times 2+8 }{ 2-2 } =\frac { 2^{ 2 }-6\times 2+8 }{ 0 } \quad \rightarrow \quad 計算不能 \)
この関数を因数分解で展開して計算すると
\(\displaystyle f(x)=\frac { { x }^{ 2 }-6x+8 }{ x-2 } \quad \quad \rightarrow \quad \quad f(x)=\frac { \left( x-2 \right) \left( x-4 \right) }{ x-2 } \quad \quad \rightarrow \quad \quad f(x)=x-4\)
となります。この展開した関数に対して\(x\)を\(2\)にして計算すると\(-2\)という値を得る事が出来ます。つまり\(x\)が\(2\)の時の値は存在しないが「確実に存在する」のです
これをプロットすると以下の表に、グラフにすると下図の様になります
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 |
| \(f(x)\) | -4 | -3 | | -1 | 0 | 1 |
| \(x-4\) | -4 | -3 | -2 | -1 | 0 | 1 |
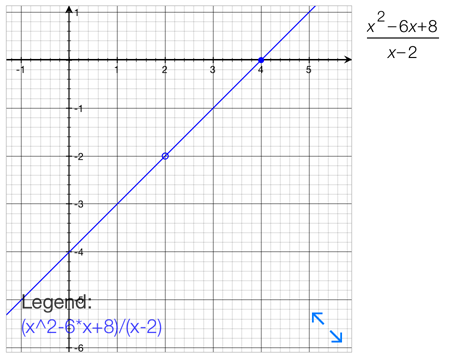
このグラフの(2,-2)が白丸になっているのは、この一点だけがグラフの線から抜けている(存在しない)事を表しています
ただ、この点はほぼ確実にある事が我々には判っています。こういう状況の時に極限を使います
\(\displaystyle \lim _{ x\rightarrow 2 }{ \frac { { x }^{ 2 }-6x+8 }{ x-2 } =-2 } \)
このように\(x\)を極限まで\(2\)に近づけ「存在しないが確実にある値」を数式を使って表現する事が出来ます
(xは2にはなっていない。あくまで極限まで近づけている)
<tips>
変数をある値に限りなく近づけると分子、分母が\(0\)に近づく場合を「\(\frac { 0 }{ 0 }\)型極限 」と呼びます。この対処法は
①分母を0にする要因を取り除く
②極限で近づく値を代入する
事で計算可能となります