高校数学​/対数

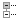
対数

対数は以上のような式で表される。累乗根は式を組んだ段階で未知数
機能的には指数法則や常用対数表などを利用して答えを導き出す。一種の関数として扱う（sin、cos等の三角関数等に似た指数関数と呼ばれるもの）
底の数を何回掛ければ真数になるか？（底を何乗すれば真数になるか？）、この場合10を3乗すれば1000になる事を表している
つまり、未知数（累乗根）が判明している段階では式的に \({10}^{3}=1000\) や \(\sqrt [ 3 ]{ 1000 } =10\) と同じ事を表現していると考えても良い

＜計算例＞

\(\displaystyle\log _{ 10 }{ 1000000 } =6\\ \log _{ 10 }{ 15 } =\log _{ 10 }{ (1.5\times 10) } =(0.176+1)\simeq 1.176\\ \log _{ 10 }{ 0.1234 } =\log _{ 10 }{ (1.234\times { 10 }^{ -1 }) } =(0.0913...+(-1))\simeq -0.9087...\\ \log _{ 2 }{ 8 } =3\\ \displaystyle\log _{ 2 }{ 100 } =\frac { \log _{ 10 }{ (100) } }{ \log _{ 10 }{ (2) } } =\frac { 2 }{ 0.3010... } \simeq 6.645...\)

\(\displaystyle\log _{ 0.9 }{ 0.5 } =\frac { \log _{ 10 }{ 0.5 } }{ \log _{ 10 }{ 0.9 } } =\frac { \log _{ 10 }{ (5\times { 10 }^{ -1 }) } }{ \log _{ 10 }{ (9\times { 10 }^{ -1 }) } } \simeq \frac { 0.699...+(-1) }{ 0.954...+(-1) } \simeq \frac { -0.301... }{ -0.0457... } =6.58...\)

＜要点＞

• 「指数」計算を機能拡張したものが「対数」
• 小数点付きの指数、負号のついた指数、有理数表現された指数との連携で対数が利用される
• 底が10の対数は常用対数と呼ばれ計算機等で利用できる

＜利点＞

• 掛算・割算の計算が対数の性質を利用する事で足算・引算に変換できる。うまく利用すると精度と引き換えに膨大な計算をキャンセルできる

計算例：
\(291765314896253\times 214281632125678926\div 12963218936134\times 3.56\div 0.0748\\ =\log _{ 10 }{ (2.917\times { 10 }^{ 14 }) } \times \log _{ 10 }{ (2.142\times { 10 }^{ 17 }) } \div \log _{ 10 }{ (1.296\times { 10 }^{ 13 }) } \times \log _{ 10 }{ (3.56) } \div (7.48\times { 10 }^{ -2 })\\ \simeq (0.465+14)+(0.331+17)-(0.113+13)+(0.551)-(0.874+(-2))\\ \simeq 0.465+14+0.331+17-0.113-13+0.551-0.874+2\\ \simeq 20.36 \)

従って
\(\quad { 10 }^{ 20.36 }\quad \rightarrow \quad { 10 }^{ 0.36 }\times { 10 }^{ 20 }\quad \rightarrow \quad 2.29\times { 10 }^{ 20 }\)

（常用対数表がある場合、筆算でこのような計算が可能となる。計算機の場合はそのまま計算したほうが早い）

• ある底の数の未知数である累乗根を計算によって導き出せる（例えば、\({3.5}^{n}=535\)　このnを求める事が出来る。これは様々な計算方法の中で対数が一番シンプルに導き出せる）

計算例1：

\({ 3.5 }^{ n }=535\quad \rightarrow \quad \log _{ 10 }{ { 3.5 }^{ n } } =\log _{ 10 }{ 535 } \quad \rightarrow \quad n\log _{ 10 }{ { 3.5 } } =\log _{ 10 }{ (5.35\times { 10 }^{ 2 }) } \\ n=\frac { \log _{ 10 }{ (5.35\times { 10 }^{ 2 }) } }{ \log _{ 10 }{ { 3.5 } } } \simeq \frac { 0.728+2 }{ 0.544 } \simeq \frac { 2.728 }{ 0.544 } \simeq 5.015\\ 従って{ 3.5 }^{ 5.015 }\simeq 535\)

（この計算は対数を利用しない場合、非常に導出が困難になる。その意味で対数の有効性が良く分かる例と言える）

計算例1：

\({ r }^{ 2 }=96364838561\\ \rightarrow \quad \log _{ 10 }{ { r }^{ 2 } } =\log _{ 10 }{ 96364838561 } \\ \rightarrow \quad 2\log _{ 10 }{ { r } } =\log _{ 10 }{ (9.636 } \times { 10 }^{ 10 })\\ \rightarrow \quad \log _{ 10 }{ { r } } =\frac { \log _{ 10 }{ (9.636 } \times { 10 }^{ 10 }) }{ 2 } \quad \rightarrow \quad \log _{ 10 }{ { r } } \simeq \frac { 0.984+10 }{ 2 } \simeq 5.492\\ 従って\quad \log _{ 10 }{ { r } } \simeq 5.492\quad \rightarrow \quad r\simeq { 10 }^{ 5.492 }\quad \rightarrow \quad r\simeq { 10 }^{ 0.492 }\times { 10 }^{ 5 }\simeq 3.10\times { 10 }^{ 5 }\simeq 310000\)

（対数と指数の関係を利用して平方根や累乗根の値を計算する事も出来る。これは対数の有効な使い方のひとつ）

＜主な用途＞

• n進数として扱う際のその数の桁数を知る事ができる
• 莫大な桁数の四則演算を必要な精度で短時間に計算できる
• 未知数である累乗根を求める計算を対数を利用することで円滑に行える

＜欠点＞

• ある程度、精度が必要な場合、対数表、計算尺、計算機が必要になる

＜tips＞

• 計算機で対数を求める際は \(\log _{ x }{ y } =\frac { \log _{ 10 }{ y } }{ \log _{ 10 }{ x } } \) の公式を利用すると良い。たとえば \(\log _{ 2 }{ 64 } \) を求める場合、64、log、÷、2、log、＝　と計算機を押すと良い

対数法則

1. \(\log _{ a }{ a } =1\)
2. \(\log _{ a }{ 1 } =0\)
3. \(\log _{ a }{ MN } =\log _{ a }{ M } +\log _{ a }{ N } \)
4. \(\log _{ a }{ \frac { M }{ N } } =\log _{ a }{ M } -\log _{ a }{ N } \)
5. \(\log _{ a }{ { M }^{ r } } =r\log _{ a }{ M } \)

底の変換公式

\(\log _{ a }{ b } =\frac { \log _{ c }{ b } }{ \log _{ c }{ a } } \quad\) (cは任意の値でOK)

実習

\({ 2 }^{ x }=5\quad \rightarrow \quad \log _{ 2 }{ 5 } =x\quad \) と表せる。これは\(\sqrt [ 2 ]{ 5 } =x\)でもある

\({ 13 }^{ x }=8\quad \rightarrow \quad \log _{ 13 }{ 8 } =x\quad \)と表せる

これは \(\sqrt [ 13 ]{ 8 } =x\) でもある

では \(\log _{ 13 }{ 8 } =x\) を求めてみる。この式は \(x=\log _{ 10 }{ 8 } \div \log _{ 10 }{ (1.3\times 10) } \)と変形できる
ここから8と1.3を対数表もしくは計算機の「log」（この場合、底は10となっている）を利用して値を引き出す
結果、1.3は0.1139...、8は0.9030...となる。これを10の指数として扱う。つまり \({ 10 }^{ 0.1139 }=1.3\) であり \({ 10 }^{ 0.9030 }=8\)となっている
ここから指数法則、対数法則を利用して計算すると \(x=\log _{ 10 }{ 8 } \div \log _{ 10 }{ 13 } =\frac { 0.9030 }{ 0.1139+1 } \simeq 0.8107\) となる（\(\simeq\) は近似値を表す）
この値が正しいか確認する為に \({ 13 }^{ 0.8107 }\) を計算機で確かめると近似値が確認できる

1 2 3 4 5 6 7 8 9 10 11 12

- | - | | | ! !

using UnityEngine; using System.Collections; public class log1 : MonoBehaviour { void Start () { print (Mathf.Log10 (8) / Mathf.Log10 (13)); print (Mathf.Log (8, 13)); print (Mathf.Pow (13, 0.8107145f)); } }

基礎的な10までの対数の筆算の求め方

　
① \(\log _{ 10 }{ { 2 } } \)を筆算で求める
\( { 2 }^{ 10 }\simeq { 10 }^{ 3 }\quad \rightarrow \quad 1024\simeq 1000 \)　これを対数で求めると　\(\log _{ 10 }{ { 2 }^{ 10 } } \simeq \log _{ 10 }{ 10^{ 3 } } \quad \rightarrow \quad 10\log { 2 } \simeq 3\log { 10 } \quad \rightarrow \quad \log { 2 } \simeq \frac { 3\times 1 }{ 10 } \quad \rightarrow \quad \log { 2 } \simeq 0.3 \)
　
（これは、つまり\({10}^{0.3} \simeq 2\)である事を導いている）
　
　
② \(\log _{ 10 }{ { 4 } } \)を筆算で求める
\(4^{ 5 }\simeq { 10 }^{ 3 }\quad \rightarrow \quad 1024\simeq 1000\quad\)　これを対数で求めると　\(\quad \log _{ 10 }{ { 4 }^{ 5 } } \simeq \log _{ 10 }{ 10^{ 3 } } \quad \rightarrow \quad 5\log { 4 } \simeq 3\log { 10 } \quad \rightarrow \quad \log { 4 } \simeq \frac { 3\times 1 }{ 5 } \quad \rightarrow \quad \log { 4 } \simeq 0.6\)
　
（これは \({10}^{0.6} \simeq 4\)である事を導いている）
　
　
③ \(\log _{ 10 }{ { 8 } } \)を筆算で求める
\(8^{ 4 }\simeq { 4\times 10 }^{ 3 }\quad \rightarrow \quad 4096\simeq 4096\quad\)　これを対数で求めると　\(\quad \log _{ 10 }{ 8^{ 4 } } \simeq \log _{ 10 }{ 4 } \times \log _{ 10 }{ 10^{ 3 } } \quad \rightarrow \quad 4\log { 8 } \simeq \log { 4 } \times 3\log { 10 }\)
\(\log { 4 }\)　は②で求まっているので　\(\quad \rightarrow \quad \log { 8 } \simeq \frac { (0.6+3) }{ 4 } \quad \rightarrow \quad \quad \log { 8 } \simeq 0.9\)
　
（これは \({10}^{0.9} \simeq 8\)である事を導いている）
　
　

＜tips＞
10を底とした対数、2,4,8の近似値は0.3刻みと憶えると良い（おおざっぱな筆算の時に役に立つ）

人の感覚と対数

人間の感覚は「対数的」であるという説がある

もし自分の財布に100円しか持っていなくて10円を落とした場合、ちょっとショックを受ける
でも、もし一万円を持って10円落とした場合、あまりショックは受けないだろう。この場合、同じショックを受けるには財布に１万円あって千円落とすと同じくらいのショックを感じるのではないか
これを対数の式にすると

\(\log _{ 10 }{ 100 } -\log _{ 10 }{ 10 } \quad =\quad 2-1\quad =\quad 1\\ \log _{ 10 }{ 10000 } -\log _{ 10 }{ 1000 } \quad =\quad 4-3\quad =\quad 1\)

このように対数計算では同じ１となり、感受した際の感覚が同一程度になる事が対数と関係する事を予想させる
１万円で１０円を落とした場合、\(\log _{ 10 }{ 10000 } -\log _{ 10 }{ 10 } \quad =\quad 4-1\quad =\quad 3\)となり、同じような感情になる事は無い
これはオクターブの異なる同じ音階に対する感じ方や、TVゲームRPGのお金の扱いやダメージ計算にも当てはまる現象となる