高校数学​/三角関数の加法定理

三角関数の加法定理

三角関数は\(\sin { (\theta +\Delta \theta ) }\) が単純な加算である\(\sin { \theta + } \sin { \Delta \theta }\)とはならない性質がある

\(\sin { 60 } +\sin { 30 } \neq \sin { (30+60) } \quad \rightarrow \quad 0.866...+0.5\quad \neq \quad 1\)

従って関数 \(f\left( \alpha +\beta \right) \)を \(f\left( \alpha \right) \)、\(f\left( \beta \right)\)で表す定理が必要になります。今回は加算減算なので加法定理となる

\(\sin { (\alpha +\beta ) } =\sin { \alpha \cos { \beta } +\cos { \alpha } \sin { \beta } } \\ \sin { (\alpha -\beta ) } =\sin { \alpha \cos { \beta } -\cos { \alpha } \sin { \beta } } \\ \cos { (\alpha +\beta )= } \cos { \alpha } \cos { \beta } -\sin { \alpha } \sin { \beta } \\ \cos { (\alpha -\beta )= } \cos { \alpha } \cos { \beta } +\sin { \alpha } \sin { \beta } \)

単純な加算とならない確認をunityでしてみる

＜サンプルコード＞

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

- | | | - | | - ! | - ! | - ! | - ! | ! !

using UnityEngine; using System.Collections; public class SinCos1 : MonoBehaviour { Vector2 vecA, vecB, tesB, VecAdditionTheorem; float alpha, beta; void Start () { alpha = 30 * Mathf.Deg2Rad; beta = 15 * Mathf.Deg2Rad; //α位置の頂点を作成 vecA = new Vector2 (Mathf.Cos (alpha), Mathf.Sin (alpha)); //ここでvecAに単純に三角関数を加算してみる（これは正しい値にならない） tesB = new Vector2 (vecA.x + Mathf.Cos (beta), vecA.y + Mathf.Sin (beta)); //こちらは本来あるべき位置の計算 vecB = new Vector2 (Mathf.Cos (alpha + beta), Mathf.Sin (alpha + beta)); //加法定理を使って計算 VecAdditionTheorem = new Vector2 (vecA.x * Mathf.Cos (beta) - vecA.y * Mathf.Sin (beta), vecA.y * Mathf.Cos (beta) + vecA.x * Mathf.Sin (beta)); } }

デバック表示で変数の中身を確認してみる

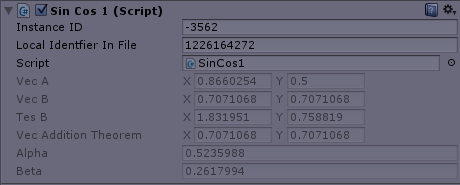
vecBとVecAdditionTheoremが同じ値になり、tesBはまったく見当違いの値になっている事が確認できる

証明1

オーソドックスな幾何図形の性質と三角関数を利用した証明

証明2

三角関数と三平方の定理の性質を利用した証明

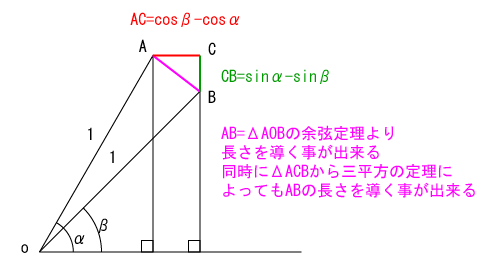
上記の図を基に証明を始める

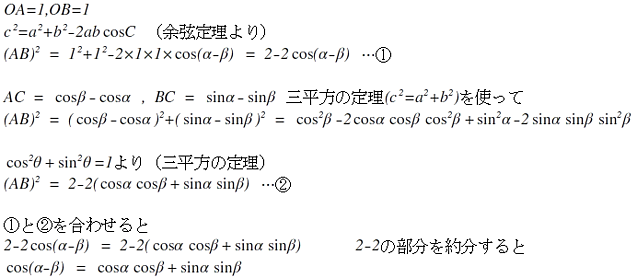
これによりcos側の証明が出来た。次にsin側の証明を行う。これには余角の公式、負角の公式を利用する

これによりsin側の証明が出来た

証明3

こちらは単位円やベクトル、三角関数の性質を利用した証明

高校数学/三平方の定理とベクトルの二点間の距離を利用する

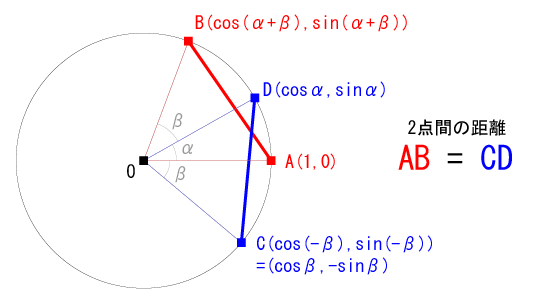
単位円上の同じ大きさを持つふたつの線分ベクトル\(\overrightarrow { AB } \)と\(\overrightarrow { CD } \)、このそれぞれの関係を式で表すと

\({ \left| \overrightarrow { AB } \right| }^{ 2 }={ \left( \cos { (\alpha +\beta ) } -1 \right) }^{ 2 }+{ \left( \sin { (\alpha +\beta ) } -0 \right) }^{ 2 }\\ { \left| \overrightarrow { CD } \right| }^{ 2 }={ \left( \cos { \alpha } -\cos { \beta } \right) }^{ 2 }+{ \left( \sin { \alpha } -\sin { \beta } \right) }^{ 2 }\)

このふたつのベクトルの式を展開する

\({ \left| \overrightarrow { AB } \right| }^{ 2 }={ \cos ^{ 2 }{ (\alpha +\beta ) } }-2\cos { (\alpha +\beta ) } +1+\sin ^{ 2 }{ (\alpha +\beta ) } \\ \quad \quad \quad =2-2\cos { (\alpha +\beta ) } \\ { \left| \overrightarrow { CD } \right| }^{ 2 }=\cos ^{ 2 }{ \alpha } -2\cos { \alpha } \cos { \beta } +\cos ^{ 2 }{ \beta } +\sin ^{ 2 }{ \alpha } +2\sin { \alpha } \sin { \beta } +\sin ^{ 2 }{ \beta } \\ \quad \quad \quad =2-2(\cos { \alpha } \cos { \beta } -\sin { \alpha } \sin { \beta } )\)

ふたつのベクトルは同じ大きさなので

\( { \left| \overrightarrow { AB } \right| }^{ 2 }={ \left| \overrightarrow { CD } \right| }^{ 2 }\\ \rightarrow \quad 2-2\cos { (\alpha +\beta ) } =2-2(\cos { \alpha } \cos { \beta } -\sin { \alpha } \sin { \beta } )\\ \rightarrow \quad \cos { (\alpha +\beta ) } =\cos { \alpha } \cos { \beta } -\sin { \alpha } \sin { \beta } \)

三角形OAB、OCDに注目すると三角形は⊿β°回転している。また頂点BDに注目すると⊿α+β°となる
これによりcos側の証明が出来た。加法と同時に減算の方も求める。これには負角の公式を利用する

\(\cos { (\alpha +\beta ) } =\cos { \alpha } \cos { \beta } -\sin { \alpha } \sin { \beta } \)
\(\beta\) を\(-\beta\) にする

負角の公式\(\cos { (-\theta ) } =\cos { \theta } ,\sin { (-\theta ) } =-\sin { \theta }\) より

\(\cos { (\alpha -\beta ) } =\cos { \alpha } \cos { (-\beta ) } -\sin { \alpha } \sin { (-\beta ) } \\ \rightarrow \cos { (\alpha -\beta ) } =\cos { \alpha } \cos { \beta } +\sin { \alpha } \sin { \beta } \)

次にsin側の証明を行う。これには余角の公式を利用する

余角の公式より\(\sin { \theta } =\cos { \left( \frac { \pi }{ 2 } -\theta \right) } \)を利用する

\(\sin { \left( \alpha +\beta \right) } =\cos { \left( \frac { \pi }{ 2 } -\left( \alpha +\beta \right) \right) } =\cos { \left\{ \left( \frac { \pi }{ 2 } -\alpha \right) +\left( -\beta \right) \right\} } \)

この式を　\(\cos { (\alpha +\beta ) } =\cos { \alpha } \cos { \beta } -\sin { \alpha } \sin { \beta }\)　に代入する

\(\sin { \left( \alpha +\beta \right) } =\cos { \left\{ \left( \frac { \pi }{ 2 } -\alpha \right) +\left( -\beta \right) \right\} = } \cos { \left( \frac { \pi }{ 2 } -\alpha \right) } \cos { \left( -\beta \right) } -\sin { \left( \frac { \pi }{ 2 } -\alpha \right) } \sin { \left( -\beta \right) } \)

余角の公式より
\(\rightarrow \sin { \left( \alpha +\beta \right) } =\sin { \alpha } \cos { \left( -\beta \right) } -\cos { \alpha } \sin { \left( -\beta \right) } \)
\(\rightarrow \sin { \left( \alpha +\beta \right) } =\sin { \alpha } \cos { \beta } +\cos { \alpha } \sin { \beta } \)
これでsinの証明が出来た

• Prev
• Next
• 高校数学